leetcode100题_last
原创Posted Updated 数据结构an hour read (About 11529 words)0 visits

leetcode100题_last

版权申明：本文为原创文章，转载请注明原文出处

原文链接：http://example.com/post/3a2a3e16.html

leetcode100题_last

2023.09.20：leetcode100题在此完结撒花o(￣▽￣)ブ

二叉树中的最大路径和（困难）

题目描述

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

img 
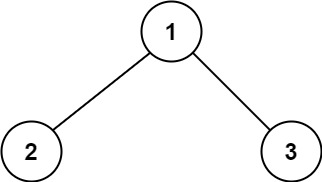
1
2
3
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

知识点

  1. 二叉树后序遍历

    1
    2
    3
    4
    5
    6
    void dfs(TreeNode*root){
        if(root==NULL)return;
        dfs(root->left);
        dfs(root->right);
        cout<<root->val;
    }

思路

首先明确我们需要求的是什么，根据题目得到，我们要求最大路径和，该路径每个节点只能出现一次，而二叉树我们对于一个节点，只有算它的左节点和右节点最方便，根据题意这条路径就两种情况：

  • 第一种：以某个节点为根节点往两边延申；
  • 第二种：以某个节点为根节点只往一边延伸；

得到这两种情况就好写代码很多，我们可以通过存储节点单项向下延申的最大值，因为对于某个根节点，如果要往两边延申，则往下延申的每个节点都只能往一边延申，而如果该根节点只往一边延伸，则往下延伸的每个节点也只能往一边延申，所以我们不需要存储该根节点往两边延伸的结果，因为后面都用不到，只需要在计算该根节点往一边延伸的最大值时顺便计算往两边延伸的最大值。

单边延伸的最大值：

1
root->val=max(max(root->left->val,root->right->val),0)+root->val;

由于我们是从下往上计算的单边延伸的最大值，所以用了后序遍历

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int maxNum=-1001;
    void maxPathForANode(TreeNode* root){
        if(root->left==NULL||root->right==NULL){
            if(root->left!=NULL||root->right!=NULL){
                if(root->left==NULL)root->val=root->val+max(0,root->right->val);
                if(root->right==NULL)root->val=root->val+max(0,root->left->val);
            }
        }else{
            maxNum=max(root->left->val+root->right->val+root->val,maxNum);
            root->val=max(max(root->left->val,root->right->val),0)+root->val;      
        }
        maxNum=max(root->val,maxNum);

    }
    void dfs(TreeNode*root){
        if(root==NULL)return;
        dfs(root->left);
        dfs(root->right);
        maxPathForANode(root);
    }
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return maxNum;
    }
};

验证二叉搜索树(中等)

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

img 
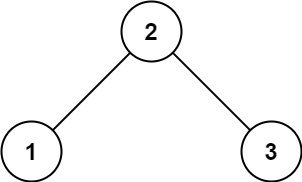
1
2
输入：root = [2,1,3]
输出：true

知识点

  1. long long最大值

    1
    long long maxnum=LLONG_MAX;

思路

这个题我们要考虑两个要点，下面我对这两个要点分别进行说明

  1. 对于一个节点，需保证左节点小于该节点，右节点大于该节点；

    这个很好实现，用前序遍历的方式，遍历每个节点，判断是否满足左节点小于该节点，右节点大于该节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    bool isValidBST(TreeNode*root){
        if(root==NULL||(root->left==NULL&&root->right==NULL))return true;
            if(root->left==NULL){
                if(root->val>=root->right->val)return false;
                return isValidBST(root->right);
            }else if(root->right==NULL){
                if(root->val<=root->left->val)return false;
                return isValidBST(root->left);
            }else{
                if(root->val>=root->right->val||root->val<=root->left->val)return false;
                return isValidBST(root->left)&&isValidBST(root->right);
            }
    }

  2. 对于一个节点，需保证左子树的所有值要大于右子树的所有值；

    这对于每个节点就需要另外的两个值，该节点需要大于的值，和该节点需要小于的值，例如，某根节点的左子节点A的右子节点B，就需要保证B的值小于根节点的值，大于A的值

    遍历方式也很简单，增加传入的参数，一个是要大于的值，一个是要小于的值，如果当前遍历节点为A，如果下一个遍历的是左节点，更新的方式是将要小于的值改成A的值，要大于的值不变，如果下一个遍历的是右节点，将要大于的值改成A的值，要小于的值不变

代码

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    bool isValidBSTForANode(TreeNode*root,long long maxnum,long long minnum){
        if(root->val<=maxnum||root->val>=minnum)return false;
        return ((root->left==NULL)?true:isValidBSTForANode(root->left,maxnum,root->val))&&((root->right==NULL)?true:isValidBSTForANode(root->right,root->val,minnum));
    }
    bool isValidBST(TreeNode* root) {
        return isValidBSTForANode(root,LLONG_MIN,LLONG_MAX);
    }
};

三数之和（中等）

题目描述

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

1
2
3
4
5
6
7
8
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

思路

好难/(ㄒoㄒ)/~~

主要就是不可以包含重复的三元组比较难满足，如果直接三次遍历不仅有可能有重复的三元组而且复杂度很高，现在考虑的就是降低复杂度，同时不要有重复的三元组

可以对原数组进行排序，这样能保证相同的数出现的地方是连续的，方便进行跳过

先对第一个数进行遍历，然后第二个数初始化为第一个数后面那个数，第三个数初始化为最后一个数，也就是最大的数，如果三个加起来比0大，第三个数就往前走，有相同的就跳过，一个数只算一次，如果加起来比0小，第二个数就往后走

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>>ans;
        int second;
        int third;
        int length=nums.size();
        for(int i=0;i<length;i++){
            while(i!=0&&i<length&&nums[i]==nums[i-1])i++;
            second=i+1;
            third=length-1;
            while(second<third){
                while(second<third&&((second!=i+1&&nums[second]==nums[second-1])||nums[second]+nums[third]+nums[i]<0)) second++;
                while(second<third&&((third!=length-1&&nums[third]==nums[third+1])||nums[second]+nums[third]+nums[i]>0)) third--;
                if(second<third&&nums[second]+nums[third]+nums[i]==0) ans.push_back({nums[i],nums[second++],nums[third--]});
            }   
        }
        return ans;
    }
};

LRU缓存（中等）

题目描述

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

思路

最近最少使用，lz仔细回忆了下os讲的内容，大概记得当时讲的是每个值会记录最近使用的时间，每次取的时候取最近使用时间最远的一次，所以我在此处也用了该思路，用了两个排序哈希（好像复杂度不满足要求？）

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class LRUCache {
public:
    int i=0;
    map<int,int>useTime;
    map<int,vector<int>>word;
    int capacityUse;
    LRUCache(int capacity) {
        capacityUse=capacity;
    }
    int get(int key) {
        if(word.find(key)==word.end())return -1;
        useTime.erase(word[key][1]);
        word[key][1]=++i;
        useTime[i]=key;
        return word[key][0];
    }
    void put(int key, int value) {
        i++;
        if(word.find(key)!=word.end()){
            useTime.erase(word[key][1]);
            word[key][0]=value;
            word[key][1]=i;   
        }else{
            if(word.size()==capacityUse){
                word.erase(useTime.begin()->second);
                useTime.erase(useTime.begin()->first);
            }
            word[key].push_back(value);
            word[key].push_back(i);
        }   
        useTime[i]=key; 
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

从前序和中序遍历序列构造二叉树（中等）

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

img 
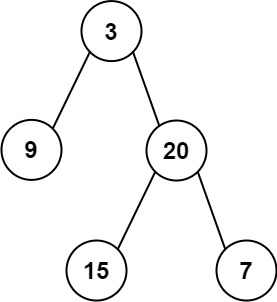
1
2
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

思路

首先明确前序序列第一个肯定是该数组表示的树的根节点，然后再inorder里面找对应的位置，该位置之前的肯定是树的左子树的中序遍历结果，之后的肯定是树的右子树中序遍历结果，同时提取出前序序列中表示左子树前序遍历结果，和右子树前序遍历结果，进行递归处理避免重复操作

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    TreeNode* buildTree(vector<int> preorder, vector<int> inorder) {
        if (preorder.empty() || inorder.empty()) return nullptr;
        TreeNode* root = new TreeNode(preorder[0]);
        for (int i = 0; i < inorder.size(); i++) {
            if (inorder[i] == root->val) {
                root->left = buildTree(vector<int>(preorder.begin() + 1, preorder.begin() + i + 1), vector<int>(inorder.begin(), inorder.begin() + i));
                root->right = buildTree(vector<int>(preorder.begin() + i + 1, preorder.end()),vector<int>(inorder.begin() + i + 1, inorder.end()));
            return root;
            }
        }
        return root;
    }
};

搜索二维矩阵（中等）

题目描述

编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

示例 1：

img 
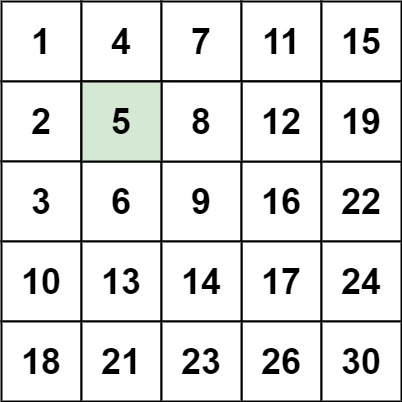
1
2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

思路(两种思路)

思路一：二分查找

先纵向遍历，只遍历比target小的，然后对那一排进行二分查找

代码一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m=matrix.size();
        int n=matrix[0].size()-1;
        int left;
        int right;
        int mid;
        for(int i=0;i<m;i++){
            if(matrix[i][0]<=target&&matrix[i].back()>=target){   
                left=0;
                right=n;
                while(left<right-1){
                    mid=(left+right)/2;
                    (matrix[i][mid]>=target)?right=mid:left=mid;
                }
                if(matrix[i][left]==target||matrix[i][right]==target)return true;
            }
            if(matrix[i][0]>target)return false;
        }
        return false;
    }
};

思路二：Z字形查找

从左下角开始，如果值比target大就往上，因为只有往上才能找到比该值小的数，如果比target小就往下

代码二

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n=matrix[0].size();
        int x=matrix.size()-1;
        int y=0;
        while(x>=0&&y<n){
            if(matrix[x][y]==target)return true;
            (matrix[x][y]>target)?x--:y++;
        }
        return false;
    }
};

N皇后（困难）

题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

img 
1
2
3
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

思路

用回溯的方法做，一排一排的放置皇后，一排只能放一个，同时为了方便确认哪些位置不能放，用了三个哈希来存不能放的位置:

  • 第一个哈希用来存放过的列，这个只需要在要放新元素的时候添加值即可
  • 第二个哈希用来放向右对角线延展的位置，因为题目要求了放了皇后的对角线位置不能放，由于可以向两边扩展对角线，所以这里用了两个哈希，同时每一排都需要更新，因为根据对角线不能放的列每一排是不一样的，往右扩展的要减一，往左扩展的要加一
  • 第三个哈希用来放向左对角线延展的位置

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
private:
    int count=0;
    vector<vector<string>>ans;
public:
    void putQueens(vector<string>ansItem,unordered_map<int,int>hash,unordered_map<int,int>hashForleft,unordered_map<int,int>hashForRight,int remainN,int n){
        if(remainN==0){
            ans.push_back(ansItem);
            count++;
            return;
        }
        unordered_map<int,int>hashForleftUse;
        unordered_map<int,int>hashForRightUse;
        for(auto it=hashForleft.begin();it!=hashForleft.end();it++){
            hashForleftUse[it->first-1]=1;
        }
        for(auto it=hashForRight.begin();it!=hashForRight.end();it++){
            hashForRightUse[it->first+1]=1;
        }
        string ansStr;
        string ansStrCopy;
        for(int i=0;i<n;i++){
            if(hash.find(i)==hash.end()&&hashForleft.find(i)==hashForleft.end()&&hashForRight.find(i)==hashForRight.end()){
                ansStrCopy=ansStr;
                ansStrCopy.push_back('Q');
                hash[i]=1;
                hashForleftUse[i-1]=1;
                hashForRightUse[i+1]=1;
                for(int j=i+1;j<n;j++){
                    ansStrCopy.push_back('.');
                }
                ansItem.push_back(ansStrCopy);
                putQueens(ansItem,hash,hashForleftUse,hashForRightUse,--remainN,n);
                hash.erase(i);
                hashForleftUse.erase(i-1);
                hashForRightUse.erase(i+1);
                remainN++;
                ansItem.pop_back();
            }
            ansStr.push_back('.');
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        unordered_map<int,int>hash;
        unordered_map<int,int>hashForleft;
        unordered_map<int,int>hashForRight;
        int remainN=n;
        vector<string>ansItem;
        putQueens(ansItem,hash,hashForleft,hashForRight,remainN,n);
        return ans;
    }
};

在排序数组中查找元素的第一个和最后一个位置(中等)

题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1
2
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

1
2
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

1
2
输入：nums = [], target = 0
输出：[-1,-1]

思路

两遍二分查找即可，第一次找左边界，第二次找右边界

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
	
    vector<int> searchRange(vector<int> nums, int target) {
        int left=0;
        int right=nums.size()-1;
        if(right<0)return{-1,-1};
        int mid;
        while(left<right-1){
            mid=(left+right)/2;
            if(nums[mid]>=target)right=mid;
            else left=mid;
        }
        int leftnum=-1;
        int rightnum=-1;
        if(nums[right]==target)leftnum=right;
        if(nums[left]==target)leftnum=left;
        left=0;
        right=nums.size()-1;
        while(left<right-1){
            mid=(left+right)/2;
            if(nums[mid]>target)right=mid;
            else left=mid;
        }
        if(nums[left]==target)rightnum=left;
        if(nums[right]==target)rightnum=right;
        return {leftnum,rightnum};
    }
};

爬楼梯（简单）

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

1
2
3
4
5
输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

思路

一次只能爬两级或者一级，那爬到第i级的总方法次数为爬到i-2级然后再爬一级加上爬到i-1级然后再爬一级

代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int climbStairs(int n) {
        vector<int>ans(n+1,0);
        ans[0]=1;
        ans[1]=1;
        for(int i=2;i<n+1;i++){
            ans[i]=ans[i-2]+ans[i-1];
        }
        return ans[n];
    }
};

完全平方数（中等）

题目描述

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

1
2
3
输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

1
2
3
输入：n = 13
输出：2
解释：13 = 4 + 9

知识点

  1. c++对数开方并往下取整

    1
    int sqrtNum=sqrt(num)

思路

很简单的动态规划,dp[i]表示第i个数的需要的最小的完全平方数,计算dp[i+1]时比较哪两个数加起来结果为i+1并且dp[j]+dp[i+1-j]值最小即需要的最小的完全平方数

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int numSquares(int n) {
        unordered_map<int,int>dp;
        for(int i=1;i<=n;i++){
            dp[i]=10000;
            for(int j=1;j<=sqrt(i);j++){
                dp[i]=min(1+dp[i-j*j],dp[i]);
            }
        }
        return dp[n];
    }
};

二叉树的直径（简单）

题目描述

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

img 
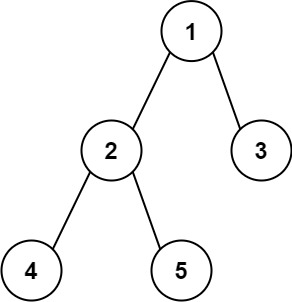
1
2
3
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

思路

之前应该做过一个很类似的题，还是用遍历加改变节点值的方法。

首先明确怎么确定这个最大路径，很简单可以思考到，这个最大路径肯定有一个'根节点'，这个根节点不一定是原二叉树的根节点，意思是从该根节点往左右节点延申到叶子节点得到的路径肯定是最长的路径，因为如果没有这个根节点，只算一边肯定不能是最大路径，因为还可以往另一边延申，如果不到叶子节点肯定也不对，因为还可以向下走，就不能算最大路径。

lz最开始的思路是用前序遍历，从根节点遍历每一个节点，算每个节点左右子树的最大高度之和就是从该根节点能达到的最大路径，但是这种方式我们每次都要重新遍历节点，每次都要重新算从某个节点往下延伸的最大高度，这样上一次算出来的最大路径在后面也不能用，所以考虑使用后序遍历的方式，先遍历最下面的，然后将算出来的高度作为节点的值，这样上面一个节点的最大路径就是左节点的高度加上右节点的高度，由于我们是从下往上算的，就不需要重复算，直接读我们存的值就可以了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
private:
    int maxNum;
public:
    void dfs(TreeNode* root){
        if(root==NULL)return;
        dfs(root->left);
        dfs(root->right);
        if(root->left==NULL&&root->right==NULL){
            root->val=0;
        }else if(root->left==NULL){
            root->val=root->right->val+1;
            maxNum=max(maxNum,root->val);
        }else if(root->right==NULL){
            root->val=root->left->val+1;
            maxNum=max(maxNum,root->val);
        }else{
            root->val=max(root->left->val,root->right->val)+1;
            maxNum=max(maxNum,root->left->val+root->right->val+2);
        }
    }
    int diameterOfBinaryTree(TreeNode* root) {
        dfs(root);
        return maxNum;
    }
};

将有序数组转换为二叉搜索树（简单）

题目描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

img 
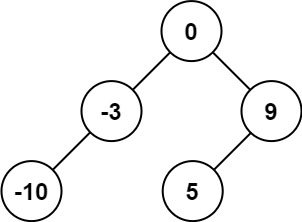
1
2
3
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

知识点

  1. vecotor重定义大小：

    1
    2
    3
    4
    5
    6
    7
    8
    vector<int>nums;
    nums.push_back(10);
    nums.push_back(2);
    nums.push_back(0);
    nums.push_back(-1);
    nums.push_bacn(-2);
    vector<int>a1(nums.begin(),nums.begin()+2);//{10,2}
    vector<int>a2(nums.begin()+2,nums.end());//{0,-1,-2}

思路

要使两边高度差小于等于1，并保证每层如此，直接将中间值作为根节点即可，每层都如此，这样能保证两边差只有1或者0

代码

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int> nums) {
        if(nums.size()==0)return NULL;
        TreeNode*newNode=new TreeNode();
        newNode->val=nums[(nums.size()-1)/2];
        newNode->left=sortedArrayToBST(vector<int>(nums.begin(),nums.begin()+(nums.size()-1)/2));
        newNode->right=sortedArrayToBST(vector<int>(nums.begin()+(nums.size()-1)/2+1,nums.end()));
        return newNode;
    }
};

环形链表（中等）

题目描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

img 
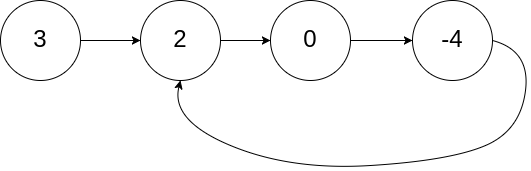
1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

思路

好吧，做完了才发现不能修改链表，还在想怎么这么简单，不修改链表的方法lz有空再做吧/(ㄒoㄒ)/~~

代码

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        while(head&&head->val<INT_MAX){
            head->val=INT_MAX;
            head=head->next;
        }
        return head;
    }
};

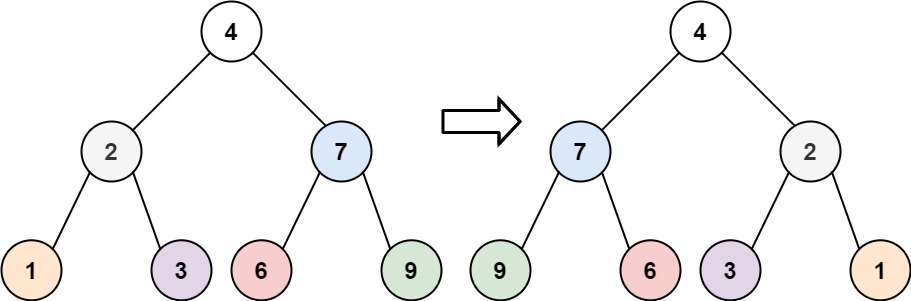
翻转二叉树（简单）

题目描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

img 
1
2
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

思路

很简单的遍历，如下代码

代码

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==NULL)return NULL;
        swap(root->left,root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

数组中第k个最大的元素(中等)（待做）

题目描述

给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

1
2
输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

1
2
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

思路：大根堆

课程表（中等）

题目描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

  • 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

知识点

  1. unordered_map合并

    1
    2
    3
    unordered_map<int, int> map1 = {{1, 10}, {2, 20}, {3, 30}};
    unordered_map<int, int> map2 = {{1, 40}, {5, 50}, {6, 60}};
    map1.insert(map2.begin(), map2.end());

思路

拓扑排序，思路就是，想象一张有向图，a->b代表完成a之后才能完成b，我们的目的就是不能在这张图中找到环

一种方法是深度优先遍历，该方法的含义首先确定一个起始节点，对其指向的节点进行深度遍历，直到遍历到没有指向的点，就说明该点课程完成之后并不能对其他课程起作用，就将该课程标记为优先级最低的那一批，也可以理解为进栈，这里的优先级最低代表该课程不会对后面进栈的所有课程起作用，但是后面进栈的课程完成之后该课程才能完成，同时遍历还有一个重要判断条件就是一个节点在一条路上不能遍历两次，否这里也比较好理解，就是我们由于是深度遍历，所以每次相当于是遍历一条路径，如果这条路径有节点遍历了两次则就说明有环，所以每遍历一条路径就需要对这条路径进行标记，这里是标记为1，同时对已经判定第优先级的节点标记为2，就相当于这条路径不会再继续往下走了，该节点也不会用了，但是该节点之前的节点还需要用，因为是深度遍历

广度优先遍历看了题解就懒得写代码了直接讲一下思路吧：还是一样的图，同时为每个节点记录入度，代表有几门课程修完之后该课程才能修，首先找到0度的节点，说明该节点可以直接修，然后从该节点进行广度优先遍历第一层，将连接的节点度数减一，相当于就是当作上一个节点直接修过了，然后在找度数为0的点继续广度优先遍历

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
private:
    vector<vector<int>> edges;
    vector<int> visited;
    bool valid = true;
public:
    void dfs(int i){
        if(!valid)return;
        visited[i]=1;
        for(int item:edges[i]){
            if(visited[item]==0){
                dfs(item);
            }else if(visited[item]==1){
                valid=false;
                return;
            }
        }
        visited[i]=2;
    } 
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        visited.resize(numCourses);
        for(auto its : prerequisites)edges[its[1]].push_back(its[0]);
        for(int i=0;i<numCourses;i++)if(!visited[i])dfs(i);
        return valid;
    }
};

分割等和子集（中等）（待做）

题目描述

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

1
2
3
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

1
2
3
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

知识点

  1. 数组求和

每日温度（中等）

题目描述

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

1
2
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:

1
2
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:

1
2
输入: temperatures = [30,60,90]
输出: [1,1,0]

思路

不知道为什么最近做题一点思路都没有，这么经典的栈题都没做出来/(ㄒoㄒ)/~~

很经典的用栈，因为要获取往后最近的比该点大的位置，开始想到了当遇到比自己小的数，就从那个数往后进行判断直到遇到比自己的大的数，但是没想起用栈/(ㄒoㄒ)/~~

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> dailyTemperatures(vector<int> temperatures) {
        vector<int>ans(temperatures.size());
        stack<vector<int>>temper;
        for(int i=0;i<temperatures.size();i++){
            while(!temper.empty()&&temper.top()[0]<temperatures[i]){
                ans[temper.top()[1]]=i-temper.top()[1];
                temper.pop();
            }
            temper.push({temperatures[i],i});
        }
        while(!temper.empty()){
            ans[temper.top()[1]]=0;
            temper.pop();
        }
        return ans;
    }
};

划分字母区间（中等）

题目描述

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

1
2
3
4
5
6
输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。

思路

想法不难，用哈希存储每个字母最后出现的次数，再通过遍历一次字符串，用双指针，如果前九个字符满足条件，只出现在这个片段中，那么可以满足哈希表中前九个字符串的所有值的最大值就是第九个字符，所以就用j来存储最大值，i来遍历，直到i等于了j就说明前j个字符的最大出现的位置就是j，那么就可以进行划分

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> partitionLabels(string s) {
        unordered_map<char,int>charToIndex;
        for(int i=0;i<s.size();i++){
            charToIndex[s[i]]=i;
        }
        int i=0;
        int j=charToIndex[s[i]];
        int num=1;
        vector<int>ans;
        while(i<s.size()){
            if(i==j){
                ans.push_back(num);
                num=1;
                if(i<s.size())j=charToIndex[s[++i]];
            }else{
                num++;
                j=max(j,charToIndex[s[i++]]);
            }
        }
        return ans;
    }
};

最长递增子序列（中等）

题目描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

1
2
3
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

1
2
输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

1
2
输入：nums = [7,7,7,7,7,7,7]
输出：1

思路

用哈希存储每个数字往前能成为严格递增序列的最大长度，对数组进行遍历，遍历的每个数字都要用哈希计算能往前构成严格递增序列的最大长度，最后记录最大的那个数也就是代码中的maxNumber，有点动态规划的感觉

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        unordered_map<int,int>numAndLength;
        int maxNumber;
        for(int num : nums){
            maxNumber=1;
            for(auto it=numAndLength.begin();it!=numAndLength.end();it++){
                if(num>it->first)maxNumber=max(it->second+1,maxNumber);
            }
            numAndLength[num]=maxNumber;
        }
        for(auto it=numAndLength.begin();it!=numAndLength.end();it++)maxNumber=max(it->second,maxNumber);
        return maxNumber;
    }
};

寻找旋转排序的最小值（中等）

题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1
2
3
输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

思路

二分法找第一个比nums[0]小的数

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findMin(vector<int>& nums) {
        int left=0;
        int right=nums.size()-1;
        int mid;
        while(left<right-1){
            mid=(left+right)/2;
            if(nums[mid]>nums[0]){
                left=mid;
            }else{
                right=mid;
            }
        }
        return min(min(nums[right],nums[left]),nums[0]);
    }
};

跳跃游戏（中等）

题目描述

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

1
2
3
输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

思路（两种思路）

思路一：用数组存储状态

从第一个下标开始，用一个额外的数组记录下能到达的位置，遍历数组，条件为该值被跳跃过就可以继续处理该值，如果遇到没有达到的值就直接返回false，说明到不了该值，那后面的值也到不了

代码一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool canJump(vector<int>& nums) {
        vector<int>numsTemp(nums.size());
        numsTemp[0]=1;
        for(int i=0;i<nums.size();i++){
            if(numsTemp[i]==1){
                for(int j=0;j+i<nums.size()&&j<=nums[i];j++){
                    if(j+i==nums.size()-1)return true;
                    numsTemp[j+i]=1;
                }
            }
        }
        return false;
    }
};

思路二：只记录能到达的最远值

index记录i+nums[i]的最大值，只要index可以到达，可以确保index之前的都能到达，如果index不能到达，说明之后的都无法到达

如果当前遍历的点小于index，说明前面就无法到达该点直接返回false，如果index比数组长度都长了说明能到达最后一个位置

代码二

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int index=0;
        for(int i=0;max(i,index)<nums.size();i++){
            if(index>=i)index=max(index,i+nums[i]);
            else return false;
        }
        return true;
    }
};

最长有效括号（困难）

题目描述

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

1
2
3
输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

思路

  1. 初始化栈（用来存字符和下标），哈希（用来存储从该点开始往前能组成的最长有效括号长度）
  2. 如果栈的最后一位是(,新进来的是)就说明这里是连续括号，但是我们不能只算这个长度，因为可能前面也有挨着的连续有效括号，这时候就需要找栈最后一位(的下标，该下标的前一位如果在哈希表中有值就说明该下标往前能组成有效括号，新进来的能组成的最长有效括号应该是前面挨着的连续的有效括号长度加上该处栈最后一位和新进来的下标差，将这个存储到哈希中以便后面还有有效括号
  3. 此外不符合条件的直接往栈里进即可

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int longestValidParentheses(string s) {
        stack<pair<char,int>>stk;
        int maxLength=0;
        unordered_map<int,int>hash;
        for(int i=0;i<s.size();i++){
            if(stk.empty()||stk.top().first!='('||s[i]!=')'){
                stk.push({s[i],i});
            }else{
                hash[i]=i-stk.top().second+1;
                auto it=hash.find(stk.top().second-1);
                if(it!=hash.end()){
                    hash[i]+=it->second;
                }
                maxLength=max(maxLength,hash[i]);
                stk.pop();
            }
        }
        return maxLength;
    }
};

腐烂的橘子（中等）

题目描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

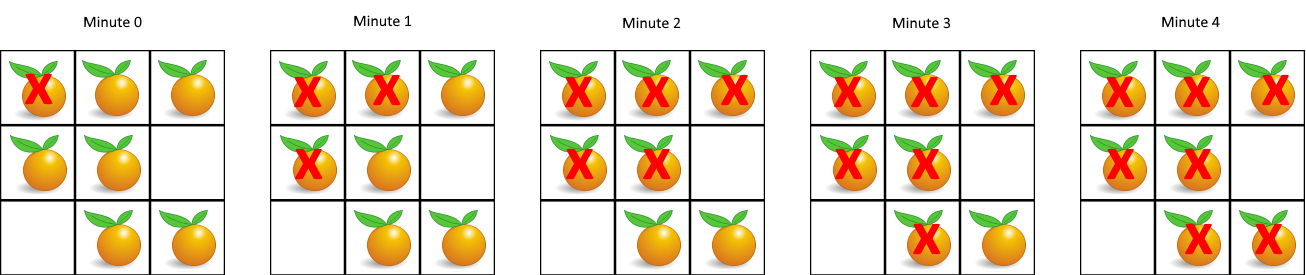
示例 1：

img

1
2
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

思路

我的思路应该就是广度优先吧（/(ㄒoㄒ)/~~）

先用数组记录下本来就是腐烂的橘子的位置，然后遍历数组并用新数组来记录上个数组记录的位置往周围扩展一层的位置，再将这个新数组赋给上一个遍历的数组，遍历完一次count+1，直到新数组的长度为零说明全都遍历完了，最后遍历一次网格如果还有新鲜水果就返回-1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {

public:
    int orangesRotting(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        int count=-1;
        vector<vector<int>>buf;
        vector<vector<int>>buff;
        vector<vector<int>>visited(m,vector<int>(n));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]==2){
                    buf.push_back({i,j});
                    visited[i][j]=1;
                }
            }
        }
        while(!buf.empty()){
            for(auto its : buf){
                if(its[0]-1>=0&&grid[its[0]-1][its[1]]!=0&&visited[its[0]-1][its[1]]==0){
                    buff.push_back({its[0]-1,its[1]});
                    visited[its[0]-1][its[1]]=1;
                    grid[its[0]-1][its[1]]=2;
                }
                if(its[0]+1<m&&grid[its[0]+1][its[1]]!=0&&visited[its[0]+1][its[1]]==0){
                    buff.push_back({its[0]+1,its[1]});
                    visited[its[0]+1][its[1]]=1;
                    grid[its[0]+1][its[1]]=2;
                }
                if(its[1]+1<n&&grid[its[0]][its[1]+1]!=0&&visited[its[0]][its[1]+1]==0){
                    buff.push_back({its[0],its[1]+1});
                    visited[its[0]][its[1]+1]=1;
                    grid[its[0]][its[1]+1]=2;
                }
                if(its[1]-1>=0&&(grid[its[0]][its[1]-1]!=0)&&(visited[its[0]][its[1]-1]==0)){
                    buff.push_back({its[0],its[1]-1});
                    visited[its[0]][its[1]-1]=1;
                    grid[its[0]][its[1]-1]=2;
                }
            }
            count+=1;
            buf.assign(buff.begin(),buff.end());
            buff.clear();
        }
        for(auto its : grid){
            for(int it : its){
                if(it==1)return -1;
            }
        }
        return count==-1?0:count;
    }
};

两两交换链表中的节点（中等）

题目描述

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

img 
1
2
输入：head = [1,2,3,4]
输出：[2,1,4,3]

思路

pre now nex代表三个相邻的节点，先确定pre，然后如果pre有next并且不为空，就让now=pre->next.nex=now->next，否则就返回原链表

然后就让now->next=pre,pre的next不能直接等于nex，因为可能nex也需要和nex的next进行交换，这里需要判断nex有没有next，有就指向nex的next，没有就指向nex，然后把pre放在nex，重复上面的步骤

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head==NULL||head->next==NULL){return head;}
        ListNode*res=head->next;
        ListNode*now;
        ListNode*nex;
        while(head&&head->next){
            now=head->next;
            nex=now->next;
            now->next=head;
            if(nex&&nex->next)head->next=nex->next;
            else head->next=nex;
            head=nex;
        }
        return res;
    }
};

分割回文串（中等）

题目描述

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

1
2
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

1
2
输入：s = "a"
输出：[["a"]]

知识点

  1. 截取子串

    1
    2
    3
    s.substr(pos, n)   截取s中从pos开始（包括0）的n个字符的子串，并返回

    s.substr(pos)     截取s中从从pos开始（包括0）到末尾的所有字符的子串，并返回

思路

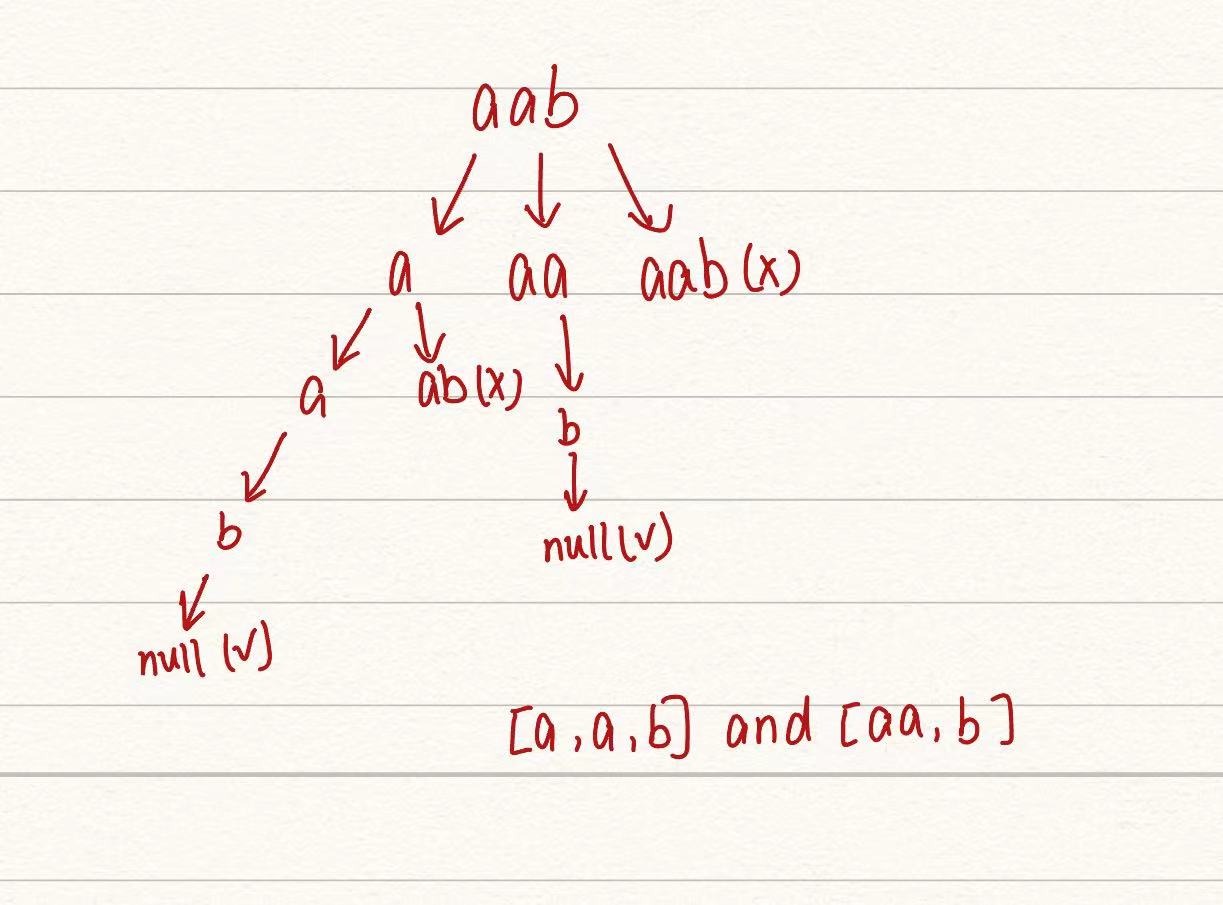
用回溯的方式去想，大概过程如图所示

5bad3ff3851a241373cd83543e10c83

从该字符串第一个字符开始，首先选一个字符，如果是回文字符串就将该字符放进返回数组列表，然后以去掉该字符的子字符串作为新字符串，以同样的方法

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    bool judgeIfHuiWen(string s){
        stack<char>stk;
        int i;
        for(i=0;i<s.size()/2;i++)stk.push(s[i]);
        if(s.size()%2){
            while(!stk.empty()&&stk.top()==s[++i])stk.pop();
        }else{
            while(!stk.empty()&&stk.top()==s[i++])stk.pop();
        }
        return stk.empty()?true:false;
    }
    vector<vector<string>> partition(string s) {
        vector<vector<string>>ans;
        string ss;
        string ss2;
        vector<vector<string>>temp;
        for(int i=0;i<s.size();i++){
            ss=s.substr(0,i+1);
            if(judgeIfHuiWen(ss)){
                ss2=s.substr(i+1);
                temp=partition(ss2);
                if(temp.size()==0){
					temp.push_back({ss});
				}else{
                    for(int j=0;j<temp.size();j++){
                        temp[j].insert(temp[j].begin(),ss);
                    }
                }
                ans.insert(ans.end(),temp.begin(),temp.end());
            }
        }
        return ans;
    }
};

矩阵置零（中等）

题目描述

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

img 
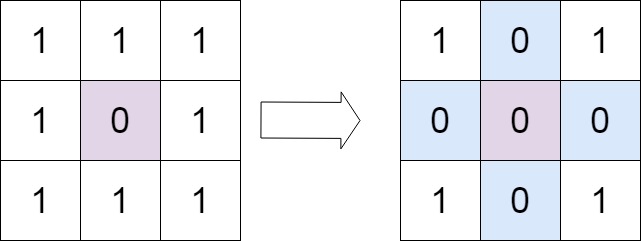
1
2
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

思路

遍历数组，如果matric[i][j]为0，就将matric[i][0]和matric[0][j]设为0，这样最后直接对第一行和第一列为0的点再对那一整行或者一整列进行归零即可，在这之前还需要记录第一行第一列是否需要置零

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int flag_col0 = false, flag_row0 = false;
        for (int i = 0; i < m; i++) {
            if (!matrix[i][0]) {
                flag_col0 = true;
            }
        }
        for (int j = 0; j < n; j++) {
            if (!matrix[0][j]) {
                flag_row0 = true;
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (!matrix[i][j]) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (!matrix[i][0] || !matrix[0][j]) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (flag_col0) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
        if (flag_row0) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
    }
};

二叉树的最近公共祖先（中等）

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

img 
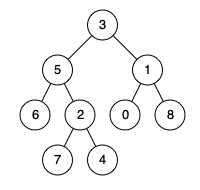
1
2
3
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

思路

从根节点开始遍历，写一个函数实现判断从该根节点往下是否存在指定节点，如果以左子节点为根节点的树存在两个节点就从该根节点继续往下遍历，如果左右都没有两个节点就说明该根节点是最深的祖先

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool ifHaveTwo(TreeNode*root,TreeNode*p){
        if(root==NULL)return false;
        if(root==p)return true;
        return ifHaveTwo(root->left,p)||ifHaveTwo(root->right,p);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while((ifHaveTwo(root->left,p)&&ifHaveTwo(root->left,q))||(ifHaveTwo(root->right,p)&&ifHaveTwo(root->right,q))){
            root=ifHaveTwo(root->left,p)&&ifHaveTwo(root->left,q)?root->left:root->right;
        }
        return root;
    }
};

二叉树的右视图（中等）

题目描述

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

img 
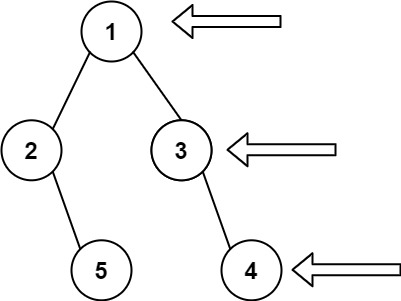
1
2
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

思路

用层次遍历的思路做，记录每一层，同时记录每一层结束的标记，遍历到一层结束的位置即存在输出数组里即可

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        TreeNode*help=new TreeNode(1000);
        vector<int>ans;
        if(root==NULL)return ans;
        queue<TreeNode*>treeQueue;
        treeQueue.push(root);
        treeQueue.push(help);
        while(treeQueue.size()>1){
            if(treeQueue.front()->left)treeQueue.push(treeQueue.front()->left);
            if(treeQueue.front()->right)treeQueue.push(treeQueue.front()->right);
            root=treeQueue.front();
            treeQueue.pop();
            if(treeQueue.front()->val==1000){
                treeQueue.push(help);
                ans.push_back(root->val);
                treeQueue.pop();
            }
        }
        return ans;
    }
};

无重复字符的最长字串（中等）

题目描述

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

1
2
3
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

1
2
3
4
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

知识点

  1. 怎么快速查找一个列表里是否有我要找的值：

    unordered_set：无序集合，它基于哈希表实现，提供了常量时间的平均复杂度进行查找、插入和删除操作。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    #include <iostream>
    #include <unordered_set>

    int main() {
        // 创建一个unordered_set用于存储字符
        std::unordered_set<char> charSet;

        // 向unordered_set中插入字符
        charSet.insert('a');
        charSet.insert('b');
        charSet.insert('c');

        // 检查字符是否存在于unordered_set中
        char target = 'b';
        if (charSet.find(target) != charSet.end()) {
            std::cout << "Character " << target << " exists in the set." << std::endl;
        } else {
            std::cout << "Character " << target << " does not exist in the set." << std::endl;
        }

        return 0;
    }

思路

用两个指针来标记无重复字符子串的头和尾，用set组合存储子串的所有元素，j每往后移一位就判断一次set组合中是否有该值，有的话i就往后移直到i遇到和j一样的元素，再往后移一位，set也将前面的元素剔除掉，取最长的set长度为五重复字符的最长字串

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int length=s.size();
        if(length==1)return 1;
        unordered_set<char>seted;
        int i=0;
        int j=1;
        int maxCount=0;
        seted.insert(s[0]);
        while(j<s.size()){
            while(j<s.size()&&seted.find(s[j])==seted.end()){
                seted.insert(s[j++]);
            }
            maxCount=max(maxCount,j-i);
            while(j<s.size()&&i!=j&&seted.find(s[j])!=seted.end()){
                seted.erase(s[i++]);
            }
            if(i==j){
                seted.insert(s[i]);
                j++;
            }
        }
        return maxCount;
    }
};

找到字符串中所有字母异位词（中等）

题目描述

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

示例 1:

1
2
3
4
5
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

思路

  1. 用哈希存储p中每个字符的状态，初始都为0
  2. 用i代表子串的头部，用j代表子串的尾部
  3. 如果s[j]在哈希表中，并且状态为0，就说明该字符在当前字串还未出现过，j就往后移动，该字符的哈希加一
  4. 如果j-i为p的长度说明已经构造除了异位词，将i存在数组中并加一，（加一之后s[i]肯定还在p中）以找下一个子串
  5. 如果s[j]不在哈希表中，i和j都要移动到j+1的位置，同时哈希初始化为0
  6. 如果s[j]在哈希表中但是已经出现过了，i就需要移动到s[j]在前面出现的位置的下一个，以确保没有出现过
  7. 同时由于p中字符会有重复，所有哈希初始化不直接为0，如果重复了再减一，后面直接判断该值是否为1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        unordered_map<char,int>hashMap;
        for(char pp : p){
            if(hashMap.find(pp)!=hashMap.end())hashMap[pp]--;
            else hashMap[pp]=0;
        }
        int i=0;
        int j=0;
        vector<int>ans;
        while(j<s.size()){
            while(j<s.size()&&hashMap.find(s[j])==hashMap.end()){
                for(int l=i;l<=j-1;l++)hashMap[s[l]]--;
                i=++j;
            }
            while(j<s.size()&&hashMap[s[j]]==1)hashMap[s[i++]]--;
            while(j<s.size()&&hashMap.find(s[j])!=hashMap.end()&&hashMap[s[j]]!=1)hashMap[s[j++]]++;
            if(j-i==p.size()){
                ans.push_back(i);
                hashMap[s[i++]]--;
            }
        }
        return ans;
    }
};

螺旋矩阵（中等）

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

img 
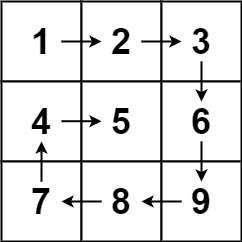
1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

思路

用up,down,left,right代表边界，比如示例从1->3遍历完之后，up要加一，代表上边界往下移了，3->9遍历完之后right要减一代表左边界往右移了，移到上下边界或者左右边界不符合不再满足小于等于关系则说明移完了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int up = 0;
        int down = matrix.size() - 1;
        int left = 0;
        int right = matrix[0].size() - 1;
        vector<int> ans;
        while (up <= down && left <= right) {
            for (int j = left; j <= right; ++j)
                ans.push_back(matrix[up][j]);
            up++;
            for (int i = up; i <= down; ++i)
                ans.push_back(matrix[i][right]);
            right--;
            if (up <= down) {
                for (int j = right; j >= left; --j)
                    ans.push_back(matrix[down][j]);
                down--;
            }
            if (left <= right) {
                for (int i = down; i >= up; --i)
                    ans.push_back(matrix[i][left]);
                left++;
            }
        }
        return ans;
    }
};

两数相加（中等）

题目描述

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

img 
1
2
3
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

思路

用两个数相加的思路，比如示例有2+5=7,进位为0，4+6+0=10，进位为1，然后3+4+1=8

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* l1Copy=l1;
        ListNode* l2Copy=l2;
        ListNode* ans=new ListNode();
        ListNode* res=ans;
        int c=0;
        while(l1Copy&&l2Copy){
            ListNode*newNode=new ListNode();
            newNode->val=l1Copy->val+l2Copy->val+c;
            if(newNode->val/10){
                newNode->val%=10;
                c=1;
            }else{
                c=0;
            }
            ans->next=newNode;
            ans=newNode;
            l1Copy=l1Copy->next;
            l2Copy=l2Copy->next;
        }
        while(l1Copy){
            ListNode*newNode=new ListNode();
            newNode->val=l1Copy->val+c;
            if(newNode->val/10){
                newNode->val%=10;
                c=1;
            }else{
                c=0;
            }
            ans->next=newNode;
            ans=newNode;
            l1Copy=l1Copy->next;
        }
        while(l2Copy){
            ListNode*newNode=new ListNode();
            newNode->val=l2Copy->val+c;
            if(newNode->val/10){
                newNode->val%=10;
                c=1;
            }else{
                c=0;
            }
            ans->next=newNode;
            ans=newNode;
            l2Copy=l2Copy->next;
        }
        if(c==1){
             ListNode*newNode=new ListNode(1);
             ans->next=newNode;
        }
        return res->next;
    }
};

排序链表（中等）

ps:实在是不想调试了，看了题解发现方法没问题就直接copy了/(ㄒoㄒ)/~~

题目描述

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

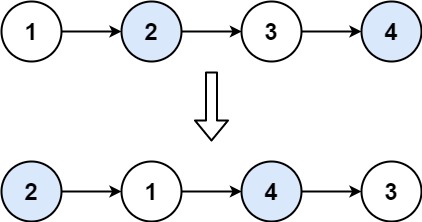
示例 1：

img 
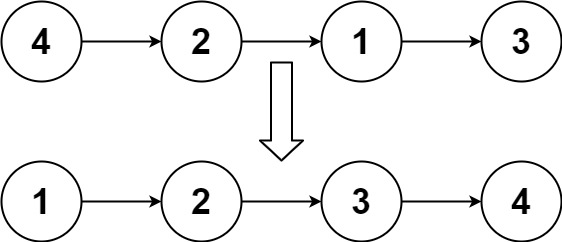
1
2
输入：head = [4,2,1,3]
输出：[1,2,3,4]

思路

归并排序，比如示例1：

[4] [2] [1] [3]

先每两个排序：

[2,4] [1,3]

再合并两个有序链表

[1,2,3,4]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (head == nullptr) {
            return head;
        }
        int length = 0;
        ListNode* node = head;
        while (node != nullptr) {
            length++;
            node = node->next;
        }
        ListNode* dummyHead = new ListNode(0, head);
        for (int subLength = 1; subLength < length; subLength <<= 1) {
            ListNode* prev = dummyHead, *curr = dummyHead->next;
            while (curr != nullptr) {
                ListNode* head1 = curr;
                for (int i = 1; i < subLength && curr->next != nullptr; i++) {
                    curr = curr->next;
                }
                ListNode* head2 = curr->next;
                curr->next = nullptr;
                curr = head2;
                for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
                    curr = curr->next;
                }
                ListNode* next = nullptr;
                if (curr != nullptr) {
                    next = curr->next;
                    curr->next = nullptr;
                }
                ListNode* merged = merge(head1, head2);
                prev->next = merged;
                while (prev->next != nullptr) {
                    prev = prev->next;
                }
                curr = next;
            }
        }
        return dummyHead->next;
    }

    ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }
};

电话号码的字母组合（中等）

题目描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

示例 1：

1
2
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

思路

很简单的回溯思路

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
private:
    vector<string>ans;
    vector<vector<char>>numToChar;
public:
    void dfs(string digits,string singleAns){
        if(digits.size()==0){
            if(singleAns.size()!=0)ans.push_back(singleAns);
            return;
        }
        for(char ch : numToChar[digits[0]-48]){
            singleAns.push_back(ch);
            dfs(digits.substr(1),singleAns);
            singleAns.pop_back();
        }
    }
    vector<string> letterCombinations(string digits) {
        numToChar.resize(10);
        numToChar[2]={'a','b','c'};
        numToChar[3]={'d','e','f'};
        numToChar[4]={'g','h','i'};
        numToChar[5]={'j','k','l'};
        numToChar[6]={'m','n','o'};
        numToChar[7]={'p','q','r','s'};
        numToChar[8]={'t','u','v'};
        numToChar[9]={'w','x','y','z'};
        dfs(digits,"");
        return ans;
    }
};

前k个高频元素（中等）

题目描述

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

1
2
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

1
2
输入: nums = [1], k = 1
输出: [1]

思路

用set集合，set放置一个元素是logn的时间复杂度，首先获取每个元素出现的次数，接着记录出现次数对应的元素，并将次数存入set，接着取set前k个数，取出次数对应元素

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int,int>numTimes;
        unordered_map<int,vector<int>>timeNums;
        vector<int>ans;
        set<int>times;
        for(int num:nums){
            numTimes[num]++;
        }
        for(auto it= numTimes.begin();it!=numTimes.end();it++){
            timeNums[it->second].push_back(it->first);
            times.insert(it->second);
        }
        for (auto it = times.rbegin();k; ++it) {
            k-=timeNums[*it].size();
            ans.insert(ans.end(),timeNums[*it].begin(),timeNums[*it].end());
        }
        return ans;
    }
};

买卖股票的最佳时机（中等）

题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

1
2
3
4
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

思路

min存储遇到的最低价格，max存储往后的最高价格，最佳时机应为前面的最低价格和遇到的最高价格之差

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProfit(std::vector<int>& prices) {
        int minPrice = prices[0];  // 初始化为第一个价格
        int maxProfit = 0;
        for (int i = 1; i < prices.size(); ++i) {
            maxProfit = max(maxProfit, prices[i] - minPrice);
            minPrice = min(minPrice, prices[i]);
        }
        return maxProfit;
    }
};

单词拆分（中等）

题目描述

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

1
2
3
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

示例 2：

1
2
3
4
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
     注意，你可以重复使用字典中的单词。

思路

首先将worddict存在set中方便查找，然后用dp[i]存储从0下标到i下标的字符串是否能够被word里的单词组成，dp[i]的更新方式是，遍历前20个字符下标，如果dp[j]为1，也就是该下标之前的都能被表示，就从该下标到i确定组成的新字符串是否在单词列表中

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string>word;
        for(string ss : wordDict){
            word.insert(ss);
        }
        vector<int>dp(s.size());
        for(int i=0;i<s.size();i++){
            for(int j=i>=20?i-20:0;j<=i;j++){
                if((j==0||dp[j-1]==1)&&word.count(s.substr(j,i-j+1))){
                    dp[i]=1;
                    break;
                }
            }
        }
        return dp[s.size()-1]==1?true:false;
    }
};

寻找重复数（中等）

题目描述

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：

1
2
输入：nums = [1,3,4,2,2]
输出：2

示例 2：

1
2
输入：nums = [3,1,3,4,2]
输出：3

思路

快慢指针

我们对 numsnums 数组建图，每个位置 iii 连一条 i→nums[i]i[i]i→nums[i] 的边。由于存在的重复的数字 targettarget，因此 targettarget 这个位置一定有起码两条指向它的边，因此整张图一定存在环，且我们要找到的 targettarget 就是这个环的入口，那么整个问题就等价于 142. 环形链表 II。

我们先设置慢指针 slowslow 和快指针 fastfast ，慢指针每次走一步，快指针每次走两步，根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇，此时我们再将 slowslow 放置起点 000，两个指针每次同时移动一步，相遇的点就是答案。

这里简单解释为什么后面将 slowslow 放置起点后移动相遇的点就一定是答案了。假设环长为 LLL，从起点到环的入口的步数是 aaa，从环的入口继续走 bbb 步到达相遇位置，从相遇位置继续走 ccc 步回到环的入口，则有 b+c=Lb+c=Lb+c=L，其中 LLL、aaa、bbb、ccc 都是正整数。根据上述定义，慢指针走了 a+ba+ba+b 步，快指针走了 2(a+b)2(a+b)2(a+b) 步。从另一个角度考虑，在相遇位置，快指针比慢指针多走了若干圈，因此快指针走的步数还可以表示成 a+b+kLa+b+kLa+b+kL，其中 kkk 表示快指针在环上走的圈数。联立等式，可以得到

1
2
2(a+b)=a+b+kL2(a+b)=a+b+kL
2(a+b)=a+b+kL

解得 a=kL−ba=kL-ba=kL−b，整理可得

1
2
a=(k−1)L+(L−b)=(k−1)L+ca=(k-1)L+(L-b)=(k-1)L+c
a=(k−1)L+(L−b)=(k−1)L+c

从上述等式可知，如果慢指针从起点出发，快指针从相遇位置出发，每次两个指针都移动一步，则慢指针走了 aaa 步之后到达环的入口，快指针在环里走了 k−1k-1k−1 圈之后又走了 ccc 步，由于从相遇位置继续走 ccc 步即可回到环的入口，因此快指针也到达环的入口。两个指针在环的入口相遇，相遇点就是答案。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int i=0;
        int j=0;
        do{
            i=nums[i];
            j=nums[nums[j]];
        }while(i!=j);
        i=0;
        while(i!=j){
            i=nums[i];
            j=nums[j];
        }
        return i;
    }
};

leetcode100题_last

http://example.com/post/3a2a3e16.html

Author

yyyyyyxnp

Posted on

2023-08-29

Updated on

2024-10-08

Licensed under

#
You need to set install_url to use ShareThis. Please set it in _config.yml.

Like this article? Support the author with

You forgot to set the business or currency_code for Paypal. Please set it in _config.yml.

Comments

You forgot to set the shortname for Disqus. Please set it in _config.yml.
Follow

Catalogue

Recents

×