原创

Explainable ML

产生原因：预测正确 != 模型有效，即希望模型能给出预测结果的支撑原因，深度神经网络对我们是一个黑盒结构，不能直接解释其结果

Interpretable vs powerful

成反比，越简单的模型解释性越强，能力越差 eg：linear model，每一个权重都有独特的含义，可用于支撑结果

越复杂的模型解释性越差，能力越强 eg：deep neural(black box)

Explainable: which is a black box, to give it the capacity for explaining

Interpretable: which is not a black box, we can gain its interpretation

Suitable choice

决策树：比线性模型能力更强，比深度神经网络更好解释。每一个节点都对应不同的问题（即特征）

但是，实际场景中，决策树用于随机森林，由多个决策树组成，难以确认模型如何确定结果

Type

• Local explaination: 即本论文所介绍的方式，即针对单个样本的解释（eg：为什么识别出图片a是数字1）
  • 方法1： 移除图片单个component，确定哪个component会影响预测结果（缺点：component过多的时候过于复杂）
  • 方法2：计算梯度：原始样本X={x1,x2,...xn...xN}--->X={x1,x2,...xn+▲x,...xN}，Jloss` = Jloss + ▲e,xn的重要性为|▲e/▲x|，我们能获得一张saliency map，每一个node代表了其重要性（缺点1：不可避免的噪声，即重点不突出，存在过多的"杂质"(用smoothGrad,对输入图片加噪声，计算map平均值)，缺点2：梯度并不能总是反映重要性，即存在这种情况： when x-->[0,x'],梯度大，when x-->[x' ,+∞]，梯度小，无法确定该特征是否影响结果）
• Global explaination：即针对预测结果的解释（eg：什么样的图片会被识别出为数字1）
  • 方法1：生成一个样本，希望模型识别出我们想要的效果（样本即为待优化参数）
  • 方法2：计算梯度上升点，但是生成的样本很有可能不符合预期（过多杂质）
  • 方法3：use a generator：input-Z(low-dim), X = G(Z), Y = D(X), 目标是min(y,yi)

More info

提升深度神经网络的可解释性是有挑战的，一种方式是训练一个更简单的解释模型(eg：linear)来模仿原始模型，确定哪些特征对模型结果产生重要影响（LIME）

Information bottleneck theory

• 互信息
  • 信息熵概念：每一件信息（事件）都有其价值，eg:从多个候选中选择答案，如果是两个候选者，选中的概率是1/2(只需要询问一次就可以获得结果，I = 1)，如果是四个候选者，选中的概率是1/4(要询问两次获得结果，I = 2)，如果是八个候选者，选中的概率是1/8(要问三次获得结果，I = 3)，因此一条信息的价值I近似为I = -log2(P)，概率越大，信息价值越小，概率越小，信息价值越大，也可称为不确定性。
    • 信息熵就是I的期望，H = ΣI*P，如果一个系统是由大量小概率事件组成，其信息熵越大，代表其不确定性越大1
  • 联合熵概念：X和Y并不独立，I(xi, yj) = -log2(P(xi, yj))，H(X,Y) = -ΣΣP(xi, yj) * log2(P(xi, yj))
    • 条件熵概念：H(X|Y)：在Y事件发生后，X事件的不确定性，即X和Y的联合熵减去Y事件本身的信息熵，就是Y发生前提下，X事件发生带来的新信息熵，H(X|Y) = H(X, Y) - H(Y)
  • 互信息概念（I(X; Y)）:I(X; Y) = H(X) - H(X|Y) = ΣP(x, y) * log2(P(x, y)/(P(x) * P(y)))，即X本身的信息熵减去Y发生后X发生带来的新的信息熵，就是X和Y的联合信息，通常来说，Y确定后，X的不确定性越大，X与Y的互信息就越少；Y确定后X越确定，X越Y的互信息越大
• 信息瓶颈理论：将神经网络视为一个encoder（X->Z）+decoder(Z->Y),目标是min(I(Z; X) - β*I(Z; Y)), 目标参数是P(Z|X)，即找到最合适的Z，最小化Z和X之间的互信息，最大化Z和Y的互信息，主要思想：将多层神经网络是为逐层传递的马尔科夫链，信息在链中被逐层压缩，去掉和输出无关的，留下和输出相关的。也就是说每一层与模型输入的互信息在逐渐减少，与模型输出的互信息逐渐增大
• 马尔科夫链：在当前条件确定情况下，未来的情况发生只取决于当前情况，和过去独立(I(X; Y|Z) = 0)
• KL散度：小概率事件包含着更大的信息价值，熵是指一个概率分布的平均信息量，用于衡量不确定性，交叉熵就是给定估计的分布概率q（预测出的）,假设真的发生的分布概率是p, 交叉熵H(p, q) = Σ pi * I(qi)，也就是真实发生的概率乘以估计的分布概率的价值，KL散度就是一种衡量真实熵和交叉熵之间的差距的方式：D(p||q) = H(p, q) - H(p) = Σpi*log(pi)/qi
  • KL散度大于等于0，只有当p=q等号成立
  • D(p||q) != D(q||p)
  • 通常使用crossentropy作为损失函数，因为我们损失函数的目的最终是梯度下降，▽D(p||qΘ) = ▽ΘH(p, q) - ▽ΘH(p) = ▽ΘH(p, qΘ)
  • 散度越小，概率越接近

VIBI(Local Explaination)

目标是既要能充分解释，又要足够简介

方法——explainer(返回每个样本被选择的概率Z,输出为T(X)=Zj*Xi)+approximator（根据解释器的输出T，模仿真实模型预测结果对模型进行训练）

现有方法——1. 针对特别的模型所构建的explainer，比如background和CNN 2.针对所有模型都可以（提供一个模型近似器）

Method

原始的信息瓶颈目标公式为 P(t|x) = argmax I(t; y) - β * I(x;t)(待优化变量：p(t|x), p(y|t), p(t))

优化目标公式为P(Z|X) = argmax(p(z|x), p(y|t)) I(t; y) - β * I(X; t)（没有p(t)的原因我猜测是因为在原始马尔科夫假设中，p(t)是表示t的边际分布，捕捉了所有可能的表示分布，但是在VIBI中，通过explainer得到了一个更具体的表示t，因此p(t)被具体的选择过程p(z|x)取代，即t由解释器P(z|x)优化，不需要再单独优化

难点：I(x; t)和I(y; t)难以直接确认，联合分布维数过高，计算代价大

首先可确定的是I(x; t)小于I(x; Z) + c(信息在传递过程是递减的，t由z和x联合计算得到，t所包含的信息是由z和x共同传递，因此t和x的信息量小于x和z的互信息量)，推理过程如下，由此，以上公式下界为以下，目标就是最大化以下

其中先验分布为均匀分布（1/length），原因如下：

1. 均匀分布假设每个特征都有相同的概率被选择，即每个特征在初始状态下是等价的。这种分布可以被视为对模型没有特定偏见的表示，保留了特征之间的潜在信息。如果使用全零向量作为先验，这意味着你假设所有特征的选择概率都是零，或者说你假设特征在初始状态下都没有信息价值。这样做会导致KL散度的值很大，因为 log_p_i 会与这个全零先验产生极大的差异，模型可能难以有效训练。
2. 在反向传播时，均匀分布能提供一个合理的梯度，使得 log_p_i 在训练过程中逐步调整，向更有意义的特征分布靠近。因为均匀分布给出的梯度不是极端的，所以有助于稳定训练。使用零向量可能会导致梯度的极端值，尤其是在KL散度的计算中。极端的梯度可能会导致训练过程中的数值不稳定，甚至梯度爆炸或消失，阻碍模型的正常学习。
3. 使用均匀分布作为先验，可以让模型从一个中立的起点开始学习，即假设每个特征最初都具有相同的重要性。这使得模型在初期阶段不会对某些特征产生偏见，从而增强了模型的泛化能力。如果使用全零向量，模型可能会被迫从一个不合理的假设出发，这可能导致过度依赖某些特征或无法充分利用所有可用信息。这样可能削弱模型的泛化能力，并导致较差的性能。
4. 均匀分布先验的假设更接近现实，因为在很多情况下，我们事先并不知道哪些特征更重要，所以均匀分布提供了一个自然的起点，减少了模型的先验偏差。零向量通常假设所有特征在初始时都是无效的，这在很多实际场景中是不合理的，可能会导致训练初期模型学习非常缓慢甚至无法学习。

难点：Pj(x) = P(zj, x)，encoder得到的是Pj(x)，要如何确定Z的值？这里的Z可看作是一个二进制列表，为1代表该块选中，实际上不能通过公式得出zj的值，我们可以通过概率进行随机采样，即使用argmax找到使得概率最大化的zj，但是argmax不可导，gumble-softmax的目标是生成一个以P为参数的公式，公式返回的结果是Z采样的结果，以便于对Z的选择可实现对P微分，可反向传播

即以连续分布去近似离散部分，softmax在一定程度上可近似argmax函数（当τ接近0时，softmax的输出近似于一个one-hot向量，其中某一个元素接近1，其余接近0，这与argmax的输出一致。）

具体方法分为两步 1. 为每个类别添加噪声（添加随机性，概率低也有可能被选中） 2. 对加噪结果应用softmax，使得结果接近原始类别分布

根据采样次数进行合并得到Z，我认为是每一次都相当于模拟一个one-hot，要找k个，就计算出k个one-hot,合并就得到最终结果，因此

最终的目标函数

实验

实验概述：训练出一个识别MNIST手写数字的模型A，查找最影响结果的输入X的四个块

对比实验设计：不进行采样（进行采样获取）和进行采样（直接选择k个概率最大的块）

Same digit, different angles.

实验结果如下图

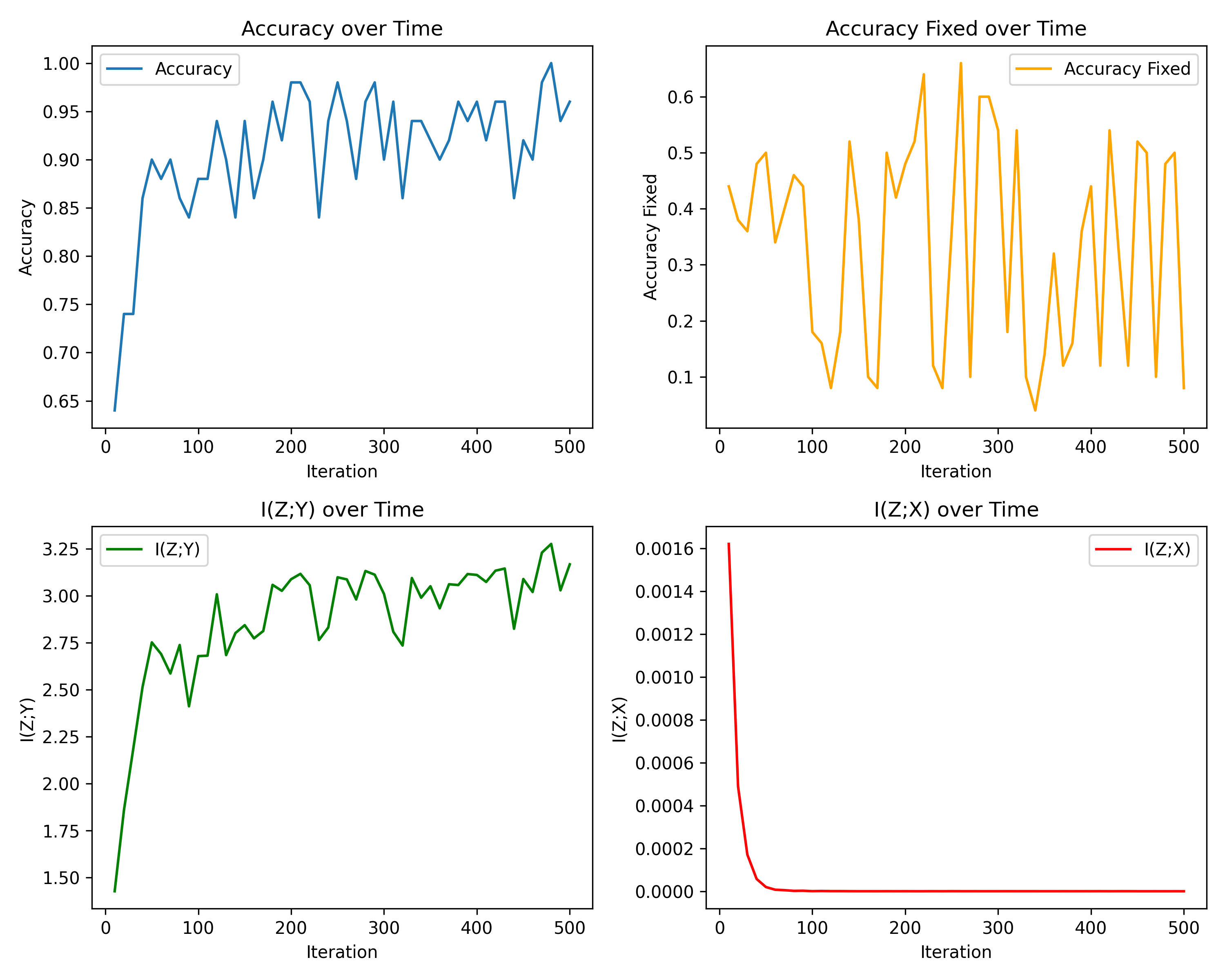
实验结果：不进行采样获取到的结果随着迭代次数增加效果越来越差，在最后几乎保持不变

进行采样和随机化后的结果准确率迅速达到饱和，且很高

原因：1. 随机性的引入 2. 后期变化小，不再进行优化