复杂网络学习
版权申明:本文为原创文章,转载请注明原文出处
复杂网络学习
前置基础知识
基本概念
Graph:指无向图(undirected Graph),即忽略了两节点间边的方向。
DiGraph:指有向图(directed Graph),即考虑了边的有向性。
MultiGraph:指多重无向图,即两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联。
MultiDiGraph:多重图的有向版本。
度:节点度是指和该节点相关联的边的条数,又称关联度。特别地,对于有向图,节点的入度 是指进入该节点的边的条数;节点的出度是指从该节点出发的边的条数。
平均路径长度:平均路径长度是拓扑网络中的一个概念,定义为所有可能的网络节点对的最短路径上的平均步数。它是网络上信息或大众运输效率的一种度量。
集聚系数:在图论中,聚类系数是图中节点聚类的程度的度量。有证据表明,在大多数真实世界的网络中,特别是在社交网络中,节点往往以相对高密度的联系为特征,形成紧密的群体;这种可能性往往大于两个节点之间随机建立平局的平均概率
节点中心性:在图论和网络分析中,中心性指标确定图中最重要的顶点。应用程序包括识别社交网络中最有影响力的人、互联网或城市网络中的关键基础设施节点和疾病的超级传播者。中心性概念最早出现在社会网络分析中,许多衡量中心性的术语反映了它们的社会学渊源。它们不应该与节点影响度量相混淆,节点影响度量试图量化网络中每个节点的影响。
复杂网络特性
- 小世界特性(Small world),即网络中点与点之间的特征路径长度值小,接近随机网络,但网络的聚合系数却很高,接近规则网络。
- 无标度特性(Scale-free),即在网络中少数节点的度值会很大,而大部分节点却很小,节点的度值分布符合幂率分布规律
- 社团结构特性,复杂网络中的节点往往会呈现出集群特性,即社团区域内部节点之间的联系非常强,而社团内节点与社团外节点的联系明显减弱。
复杂网络统计特性
平均路径长度 复杂网络里,两节点之间的最短路径上所包含的边的数目就表示两个节点之间的距离。网络中任意两个节点之间距离的平均值就是网络的平均路径长度,它代表了网络中节点间的分离程度,是网络全局特性的反映。
度、度分布、度相关性
度:复杂网络里,一个节点与网络中其他节点的连边总数就是节点的度。 度分布:网络中节点的度值按从小到大排序,统计得到度为 k 的节点占整个网络节点数的比例 P(k),就是网络的度分布(Degree distribution);从概率角度看,P(k)就是网络中随机选择一个节点,其度为 k 的概率 度相关性 同配:度大节点倾向于连接度大节点。同配网络相关性系数 > 0 异配:度大节点倾向于连接度小节点。异配网络相关性系数 < 0 中性:节点间的连接与它们自身的度值无关。中性网络相关性系数 = 0
聚集系数 复杂网络里,一个节点的邻居节点之间连边的数目占这些邻居节点之间最大可能连边数目的比例就是节点的聚集系数。网络中所有节点聚集系数的平均值就是网络的聚集系数,它反映了网络中节点的聚集情况即网络的聚集性。
介数 分为节点介数和边介数。
节点介数:指网络中所有最短路径中经过该节点的数量占总的最短路径数量的比例
边介数则指网络中所有最短路径中经过该边的数量占总的最短路径数量的比例。
确定节点重要性
- 基于网络局域特征的排序方法
- 度中心性:根据节点度数排
- 基于网络全局属性的排序方法
- 介数中心性/中介中心性 Betweenness Centrality:网络中所有的两节点间的最短路径中经过某个节点的条数越多,那么该节点就越重要。
- 紧密度中心性:计算节点到网络中的其他节点的最短距离,到其他节点的最短距离之和越小,紧密度越大,则节点就越接近网络的几何中心,节点也就越重要
- 离心中心性(Eccentricity):一个节点与网络中的所有节点的最短距离之中的最大值。点的离心中心性越小,说明越接近网络的中心,节点就越重要
- 特征向量中心性(Eigenvector Centrality):如果节点A连接并影响着节点B,而节点B被其他更多节点连接着,则节点A的特征向量中心性就很大
理解数据集内容
图像一

这张图就是将网络图像化,这里的network就是一个场景,比如在internet中,节点就是路由器,边就是网络的连接,应该就指路由器之间的拓扑连接,后面指明是有向边还是无向边,然后数据集中的节点数量,链路数量,k是一个结点的平均度数
代码部分
计算不同网络节点数,边数,平均度数
图像二
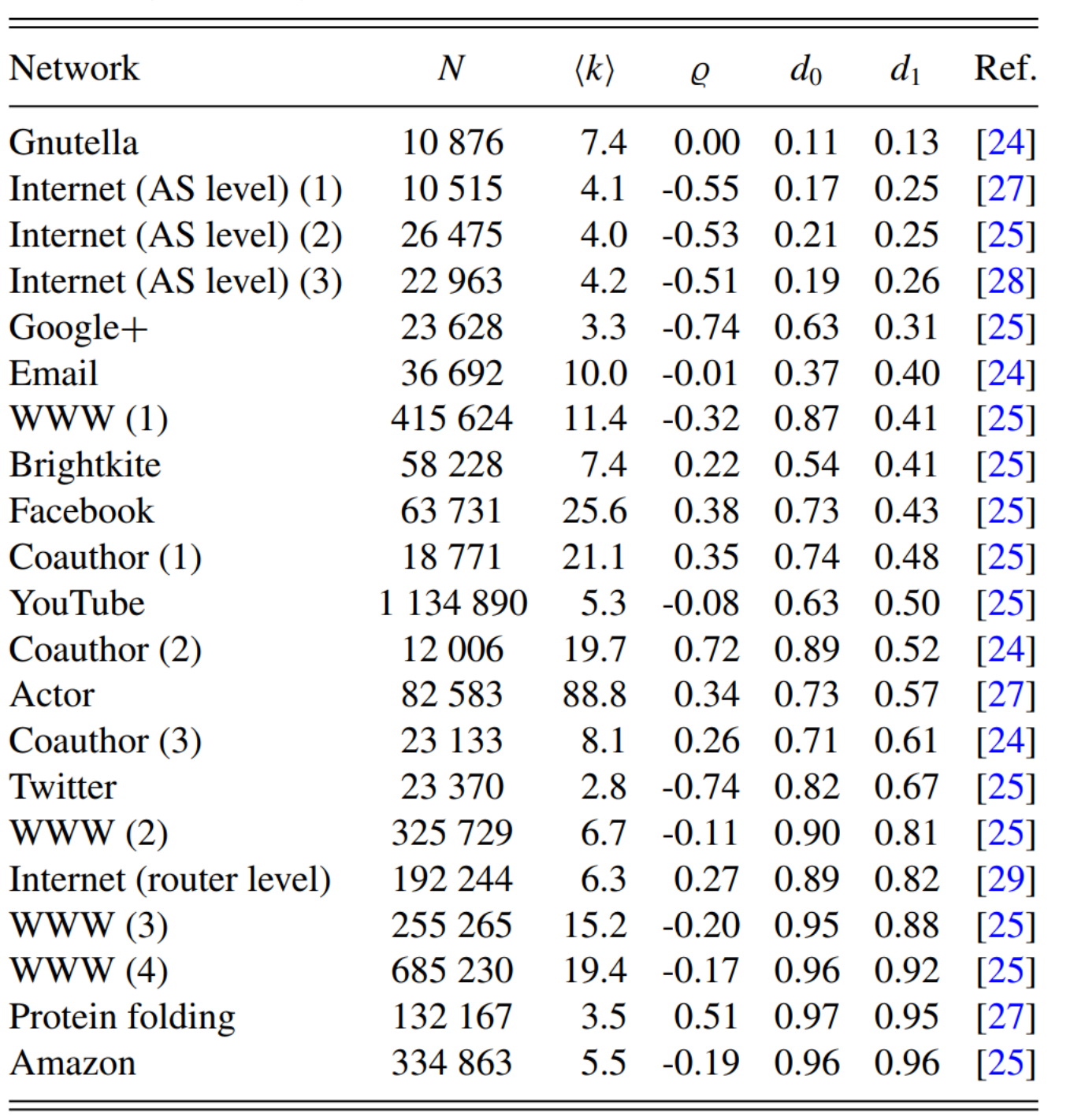
现在分析这张图,N是节点数,k是平均度数,注意无边图一条边两个节点共享,第三个字母应该是聚类系数,即一个度量图中节点之间聚集程度或紧密程度的指标,取值范围在-1到1之间。它等于所有节点局部聚类系数(即一个节点与其邻居形成三角形比例)减去随机图中期望的局部聚类系数,d0表示度数为0的节点所占的比例,d1表示度数为1的节点所占的比例
代码部分
这部分和第一张图的代码部分很相似,就是计算不同网络数据集的节点数,边数,平均度
图像三

这张图表示两个经验网络的结构特征,包括节点数N、边缘E数、平均度(K)、分类系数r和聚类系数C。分类系数是指一个节点与其邻居节点之间的平均相似度,也就是节点的一跳邻域内所有边的权重之和除以边的个数,这种定义下的分类系数可以是正数或者负数,取决于边的权重是正还是负。如果边的权重表示相似度,那么正数表示相似,负数表示不相似;如果边的权重表示差异度,那么正数表示不相似,负数表示相似。
图像四
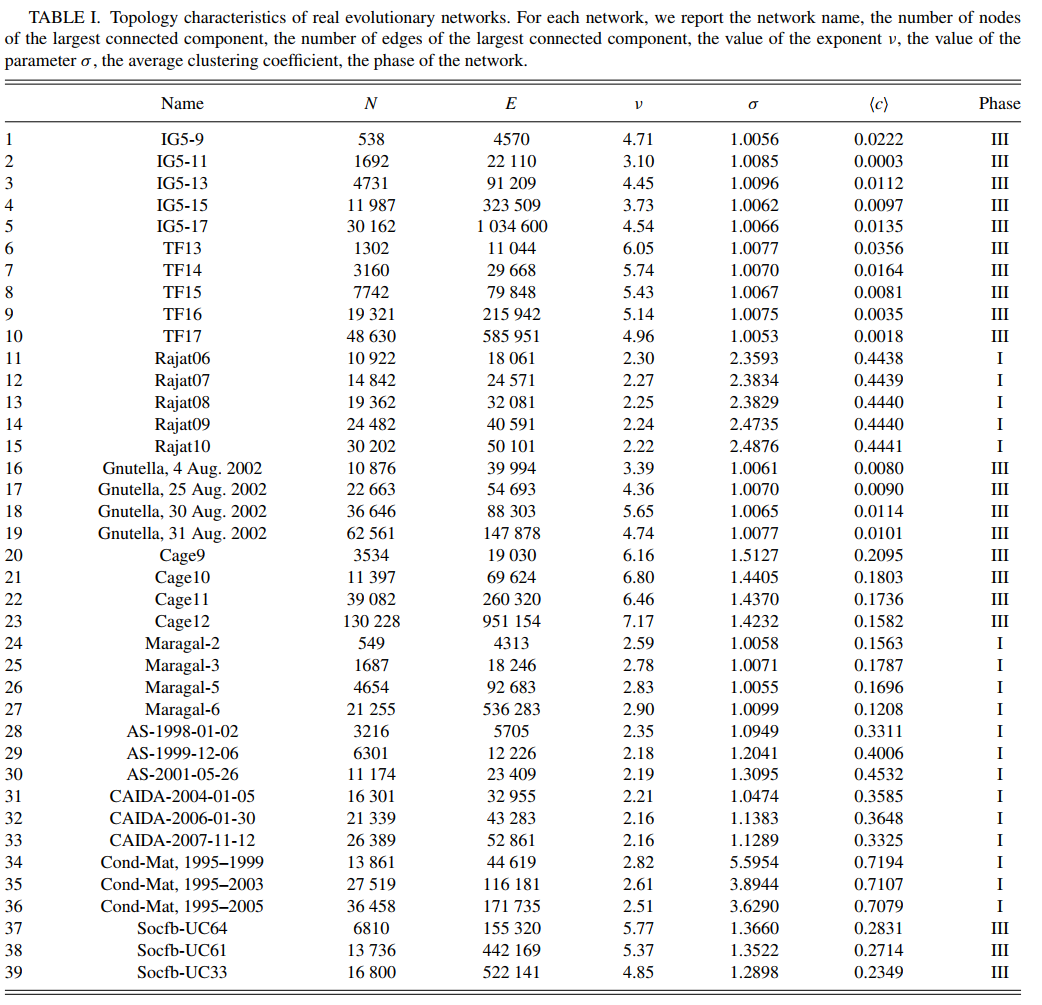
包含了网络名称、最大连通分量的节点数、最大连通分量的边数、指数v的值、参数σ的值、平均聚类系数c、网络的相位。指数v的值和参数σ的值是用来描述网络的标度律特性的指标,标度律是指网络中节点的度分布服从幂律分布,也就是说,网络中度为k的节点的数量与k的负幂成正比,指数v的值是指网络中节点度的平均值,也就是说,网络中所有节点的度之和除以节点的个数,指数v的值是指网络中节点度的平均值,也就是说,网络中所有节点的度之和除以节点的个数,参数σ的值是指网络中节点度的标准差,也就是说,网络中所有节点的度与平均度之差的平方和除以节点个数再开根号,网络的相位是指网络在不同状态下表现出不同的行为特征。一般来说,网络可以分为三种相位:有序相、临界相和混沌相。在有序相中,网络中大部分节点都处于稳定或者同步的状态,即使有少量节点发生变化也不会影响整个网络。在临界相中,网络中存在一个临界点或者临界区域,在这里网络表现出最大的复杂性和多样性。在混沌相中,网络中大部分节点都处于不稳定或者异步的状态,即使有少量节点保持不变也不会影响整个网络
图像五
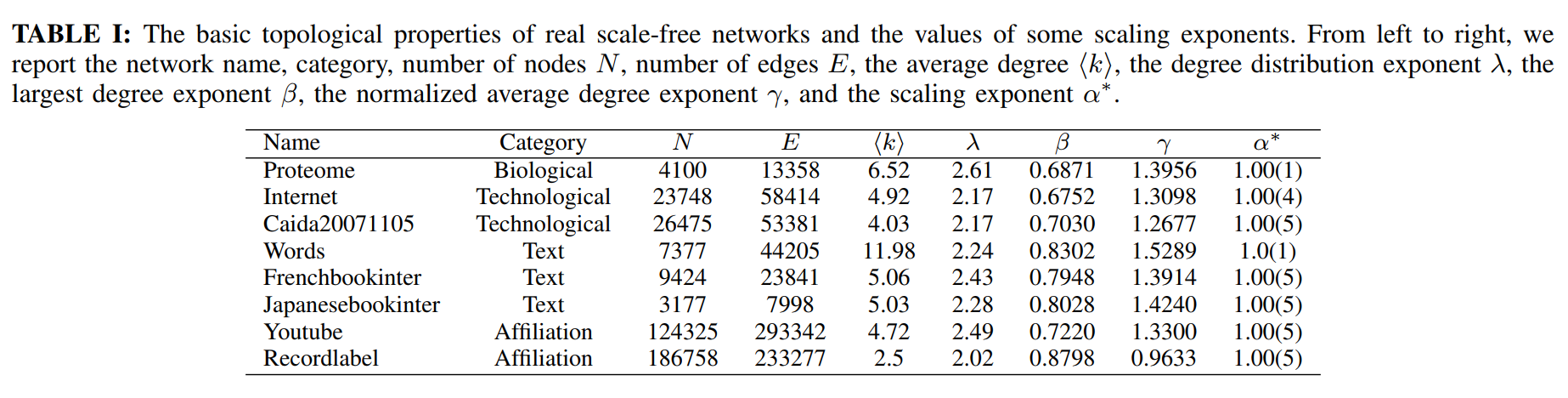
实无标度网络的基本拓扑性质和一些标度指数的值。从左到右依次为网络名称、类别、节点数N、边数E、平均度(K)、度分布指数λ、最优度指数β、归一化平均度指数γ,和标度指数a*。
解释:度分布指数λ是指网络中实际的节点度的幂律分布的指数,也就是说,网络中度为k的节点的数量与k的负λ次方成正比
归一化平均度指数γ是指网络中节点度与平均度之比的归一化处理后得到的指数,也就是说,网络中节点度为k的节点的数量与k除以平均度v再取对数后成正比
最优度指数β是指网络中节点度的最优分布的指数,也就是说,网络中度为k的节点的数量与k的负β次方成正比
a的值是1表示你的图中节点度与最小度之比再取对数后得到的指数是1,也就是说,你的图中节点度与最小度之比的对数分布是线性的
代码部分
m=2
m=5
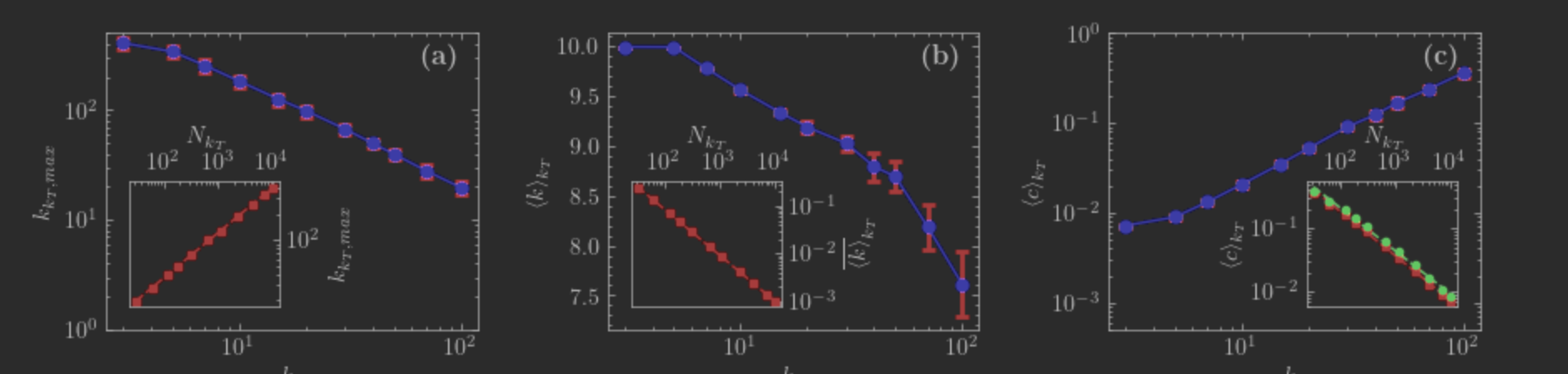
λ=2.1
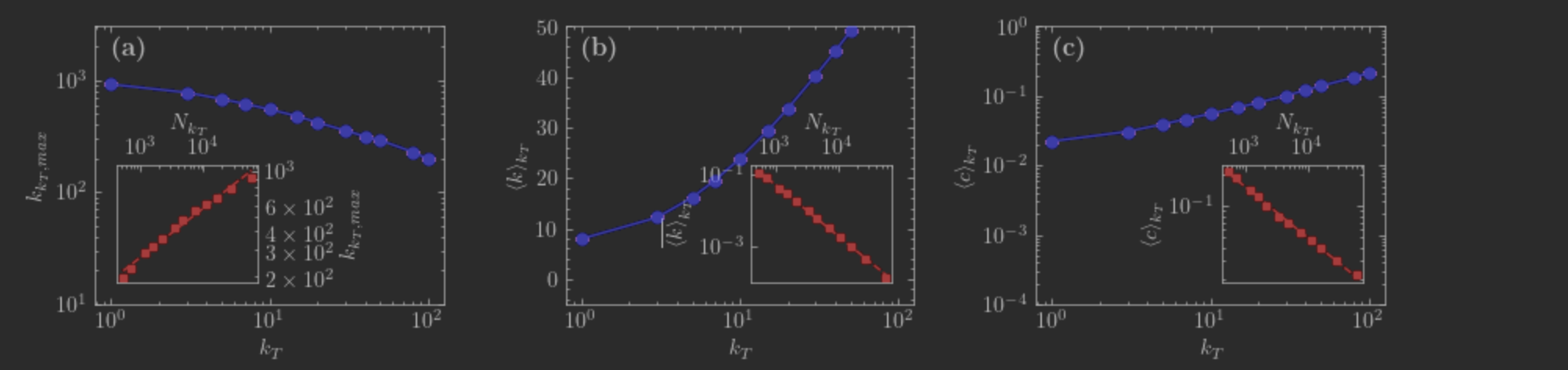
λ=2.5
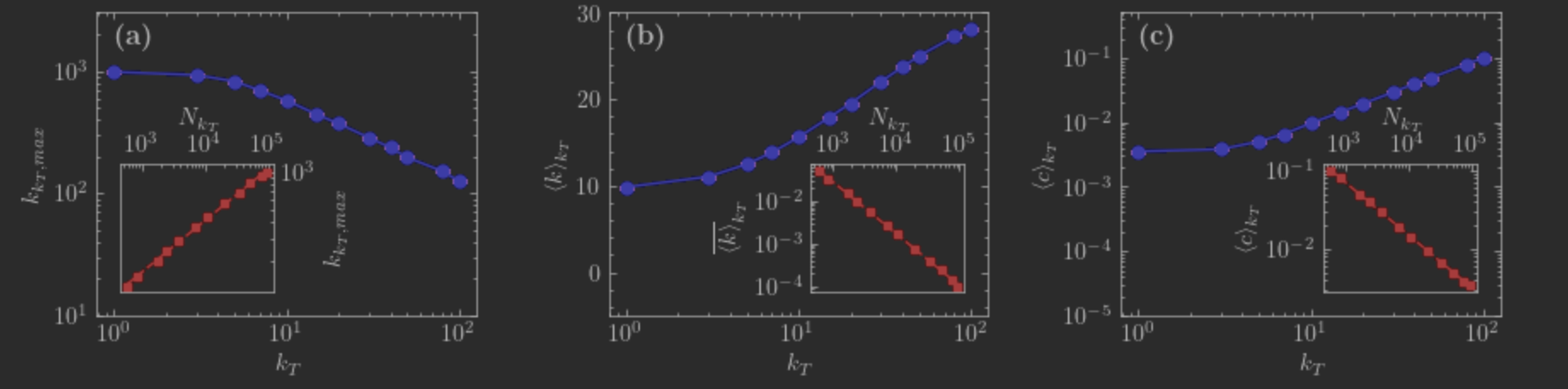
图像六
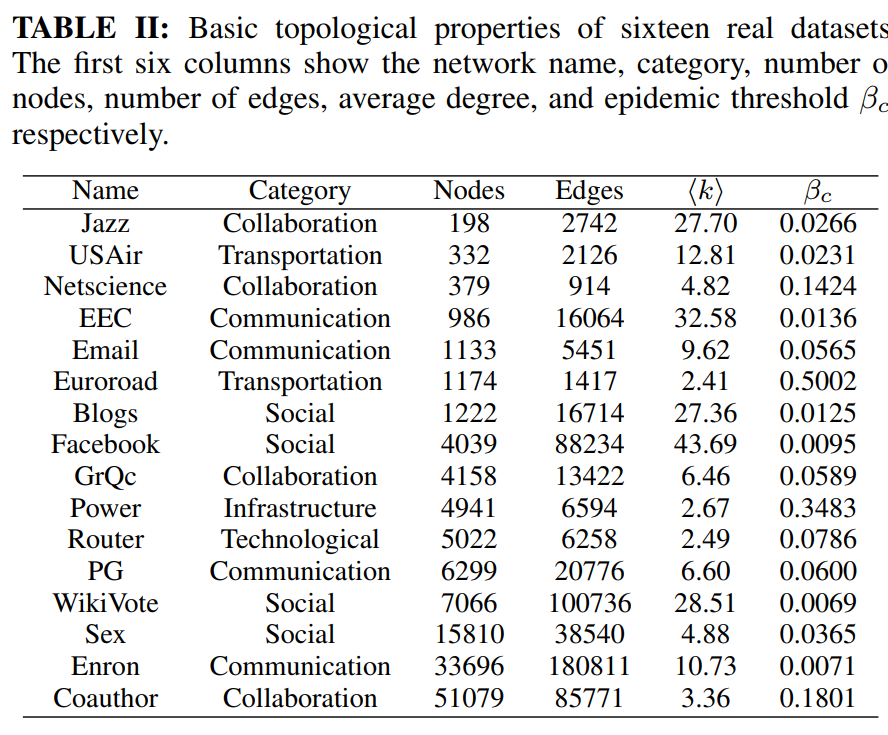
16个实数据集的基本拓扑性质前六列显示网络名称、类别、数节点、边数、平均度和epidemic threshold:βc。
βc是指一个网络中发生传染病流行的临界条件,也就是说,当传染病的传播率β超过这个临界值βc时,传染病就有可能在网络中广泛传播;当传播率β低于这个临界值βc时,传染病就有可能在网络中消失。这个临界值βc与网络的结构和拓扑性质有关,一般来说,网络中节点度的分布越不均匀,临界值βc就越低,也就是说,网络越容易发生传染病流行。图中βc的值是0点几,那么可能说明图中节点度的分布比较不均匀,也就是说,图是一个无尺度网络或者近似无尺度网络。
无尺度网络是一种复杂网络,其特点是网络中的大部分节点只和很少节点连接,而有极少的节点与非常多的节点连接。这种网络的节点度分布遵循幂律分布,也就是说,高度数的节点的概率随着度数的增加而缓慢下降,没有一个典型的平均值。无尺度网络在现实中很常见,例如万维网、社交网络、金融网络等。
代码部分
最后的代码其实就是用于评估不同的节点中心性算法和真实的中心性排名之间的相关性。
在EHCC 算法(一种网络中心性算法)中,考虑的是扩展度数而不是直接用的度数,原因:使用扩展度量的目的是为了更全面地衡量节点在网络中的重要性。虽然节点的度(degree)是一个最常见的中心性度量,但它只考虑了节点直接相邻的连接数,没有考虑到节点的邻居节点的连接情况。
文件类型解析
txt文件:
- 第一种:一行代表一条边,比如 0 1代表的是0到1有一条边,根据提示判断是否是有向边
- 第二种:一行有四个数字,前两个数字是节点的编号,第三个数字是边的权重,第四个数字是边的时间戳,表示边的创建时间。有些图的边是随着时间变化的,所以需要记录时间戳,在读取文件的时候可以用data=False,就会忽略权重和时间戳。如果你想读取权重(未解决)
gml文件:我看到的gml文件格式是:
1 | graph |
install_url to use ShareThis. Please set it in _config.yml.


