原创

计算机视觉

计算机视觉可以做到的事情(分类、识别、转换)：

image-20230711214114438

对于图片来说，越清晰的图片像素点越多，样本维度也就越大，对于过大的可以用卷积

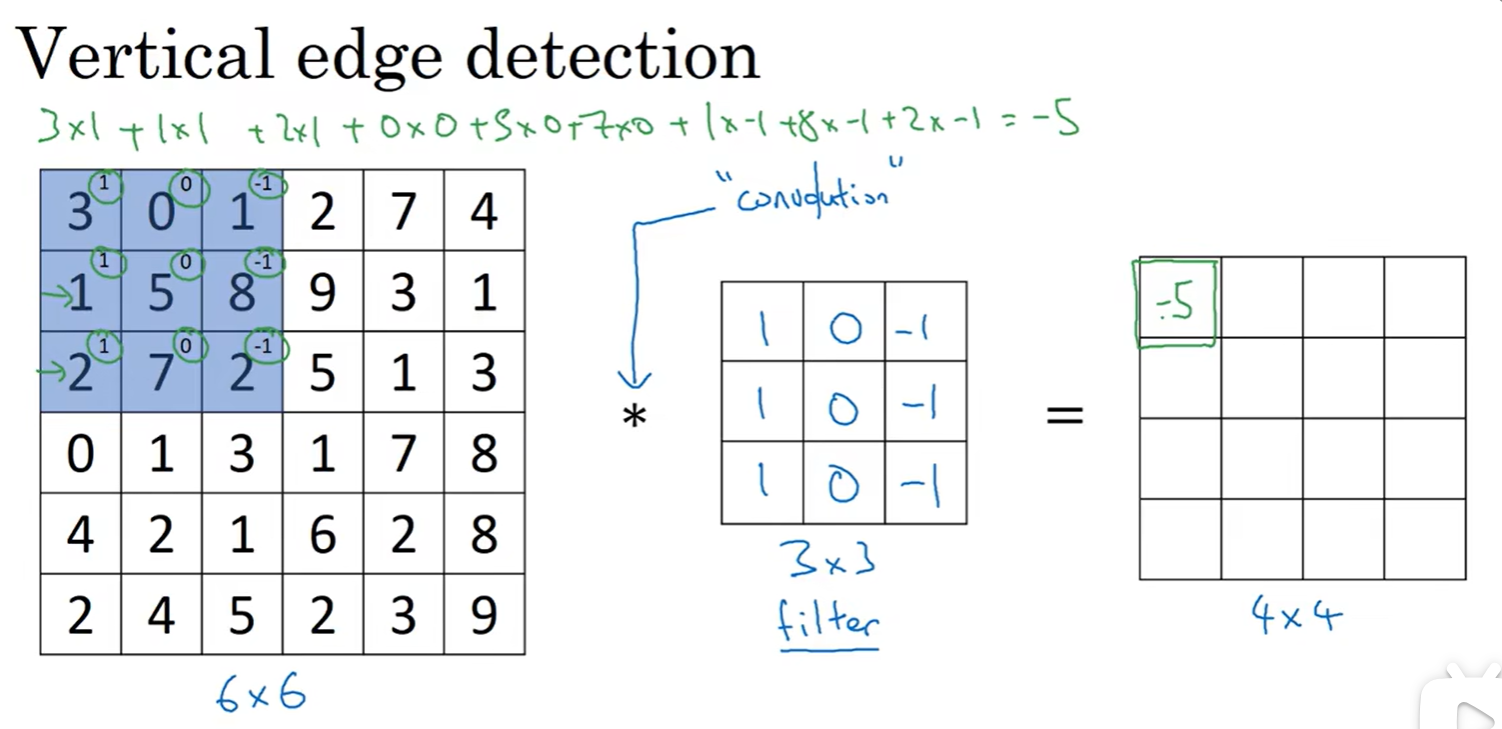
边缘检测示例

在这儿代表着卷积运算，中间那个3 3的方块相当于（垂直边缘检测器）过滤器：

image-20230711214724539

image-20230711214746368

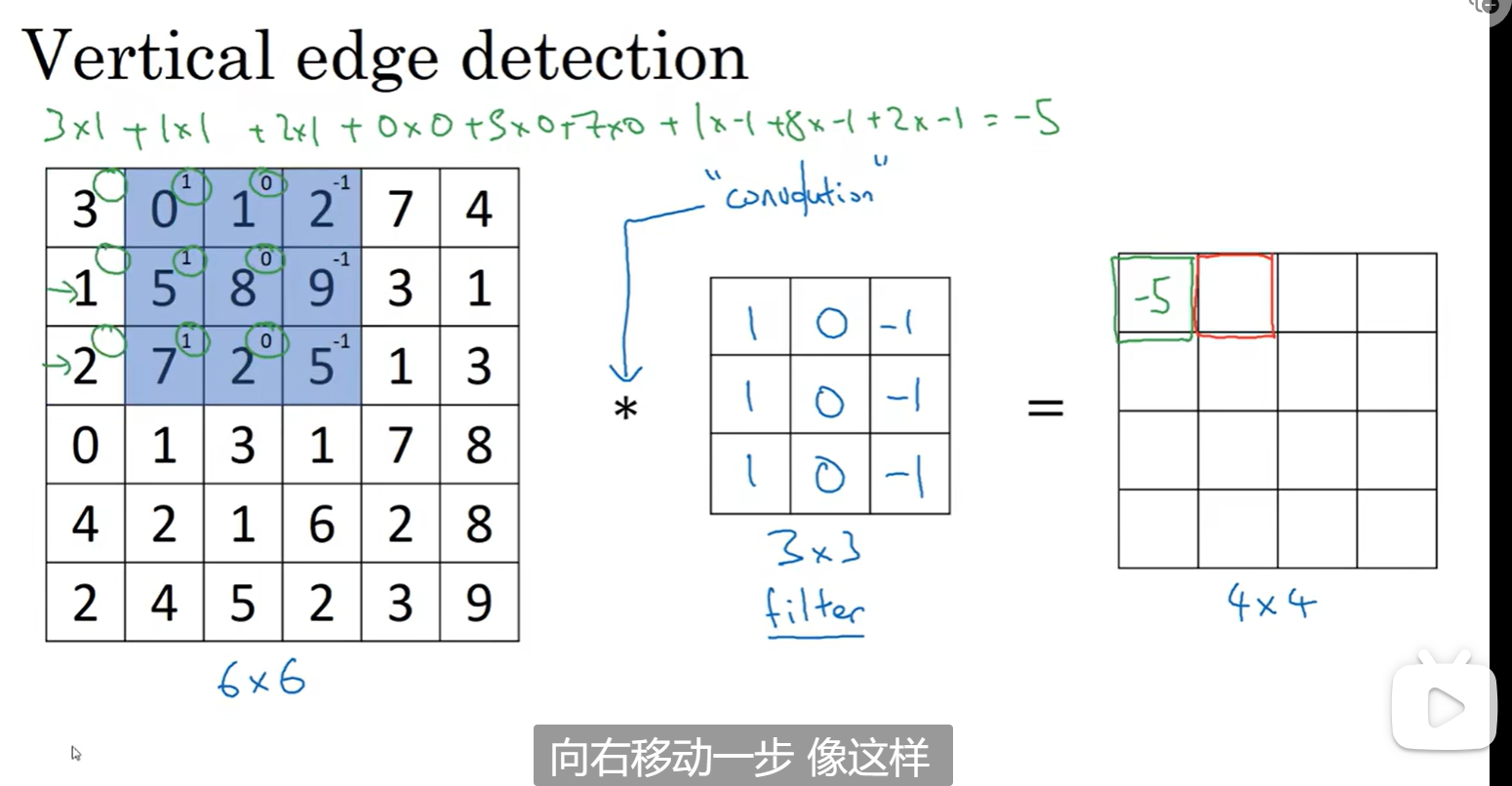
为什么可以这么做卷积(可以很好的识别出图像的垂直边缘，比如最左边的图中间是垂直边缘，然后通过卷积，可以识别出中间是边缘，中间就做了高像素处理)：

image-20230711215116492

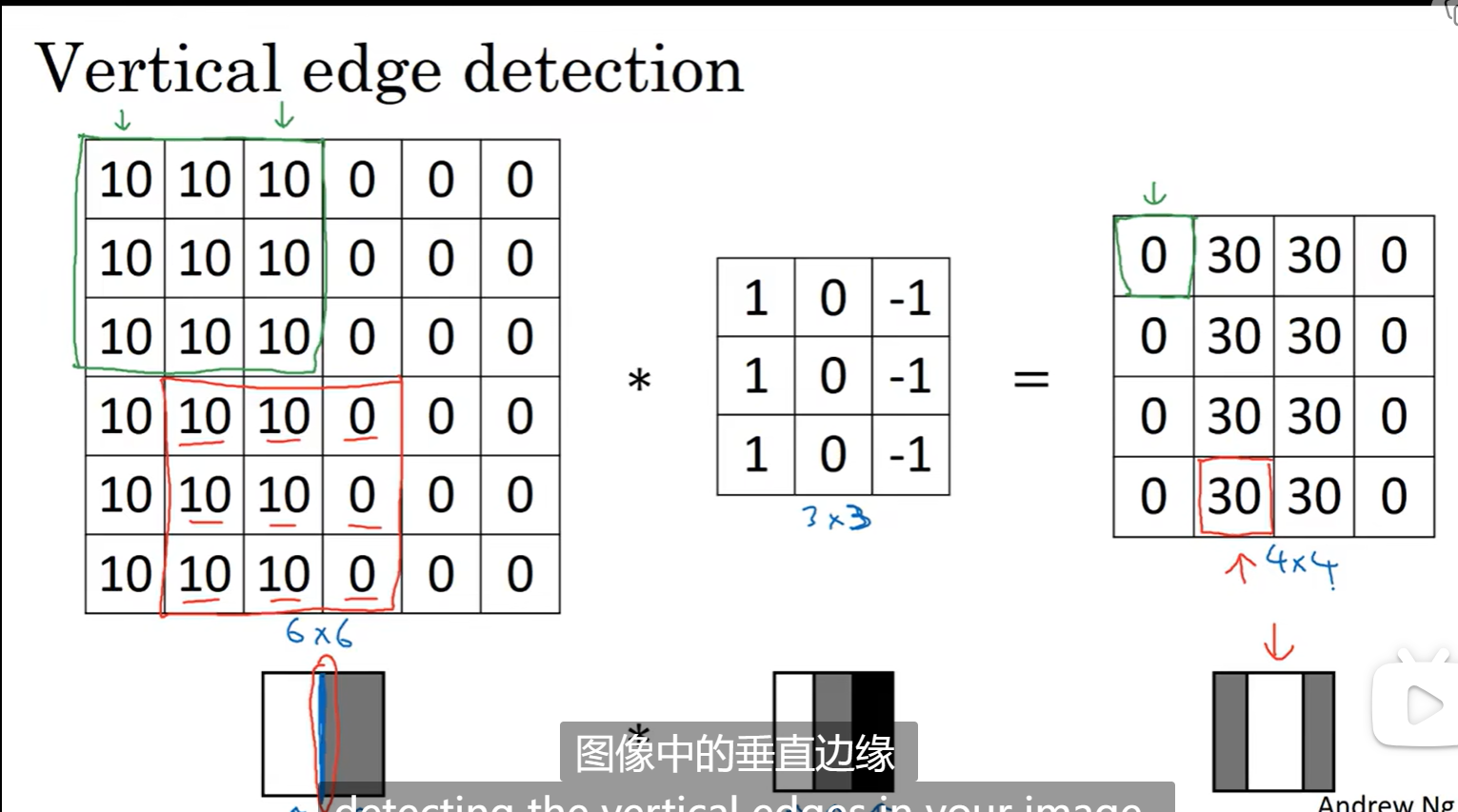
更多边缘检测内容

区分正边和负边

按照上面的类似情况还有如下（这种就需要转换为绝对值）：

image-20230711230502838

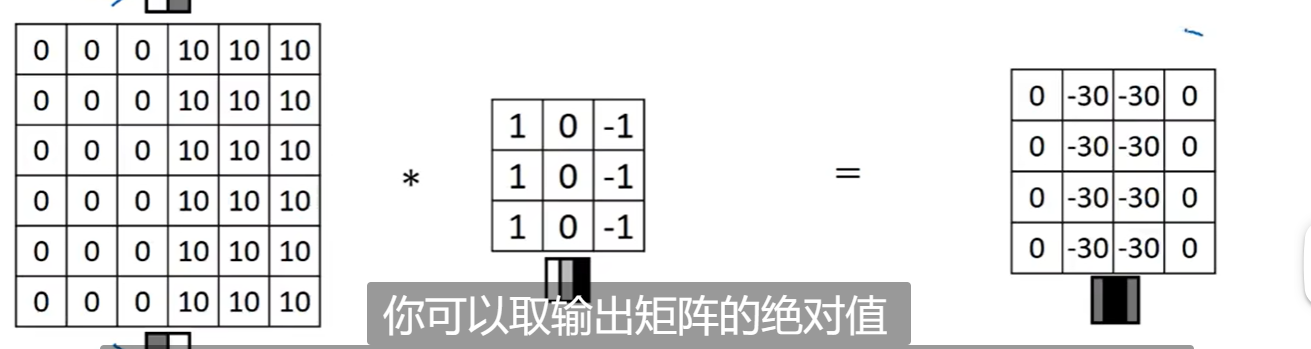
类似的还有水平边缘检测器：

1 1 1

0 0 0

-1 -1 -1

事实上存在着很多的水平或者垂直过滤器，事实上，我们不一定要照抄别人有的过滤器，我们可以通过自定义参数设置过滤器，然后通过反向传播不断更新迭代，重点就是怎么用反向传播进行更新迭代

image-20230711231148663

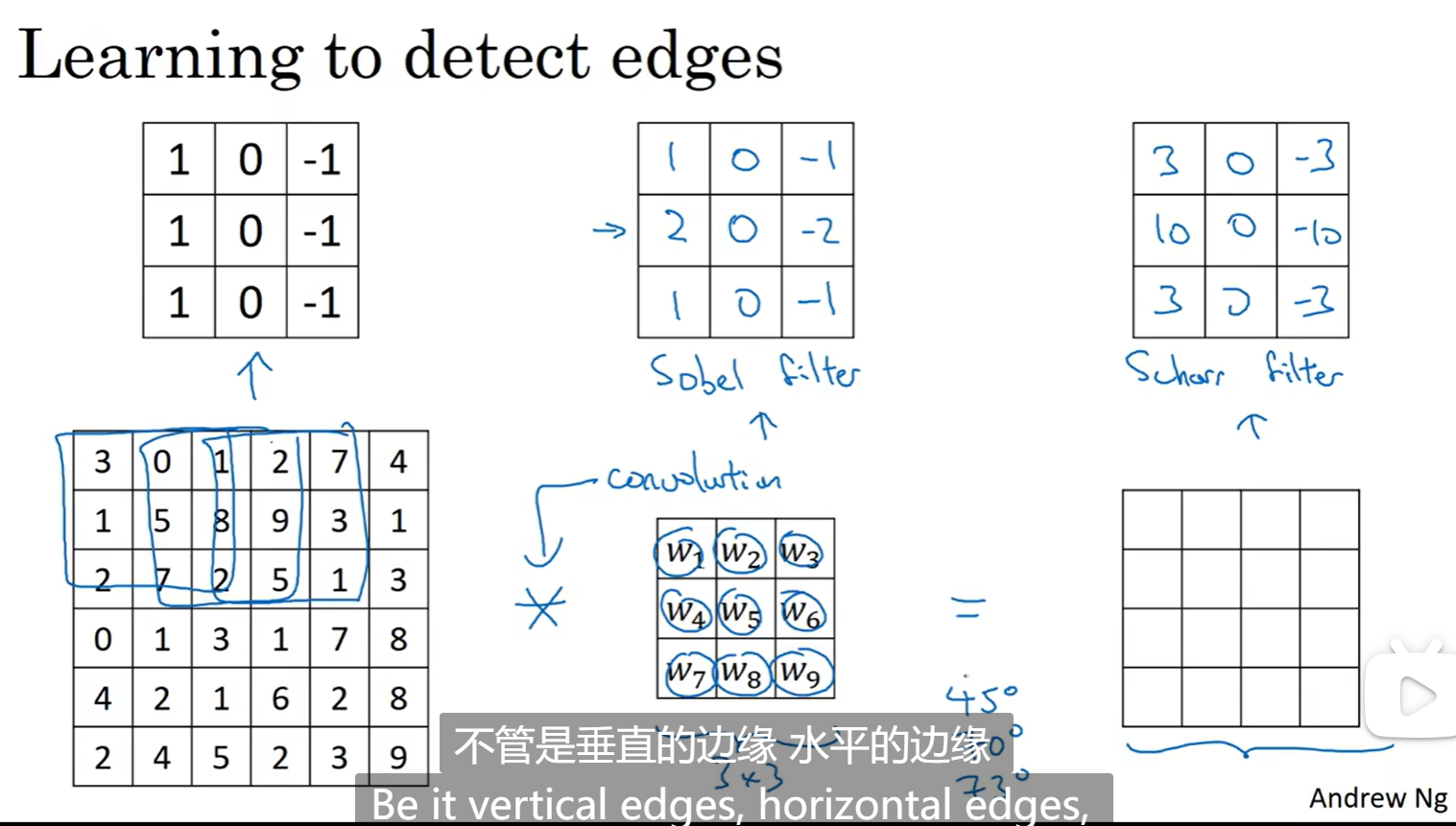
Padding

卷积的两个缺点：6 * 6的像素会变成4 * 4，元素会减少，这并不是一件好事；并且中间元素会被重复计算很多次，耳边元素只会被计算一次

方法：扩大输入图像像素点，比如下图中的p，p=1就是往外扩大一层，p=2就是往外扩大两层

image-20230711232503821

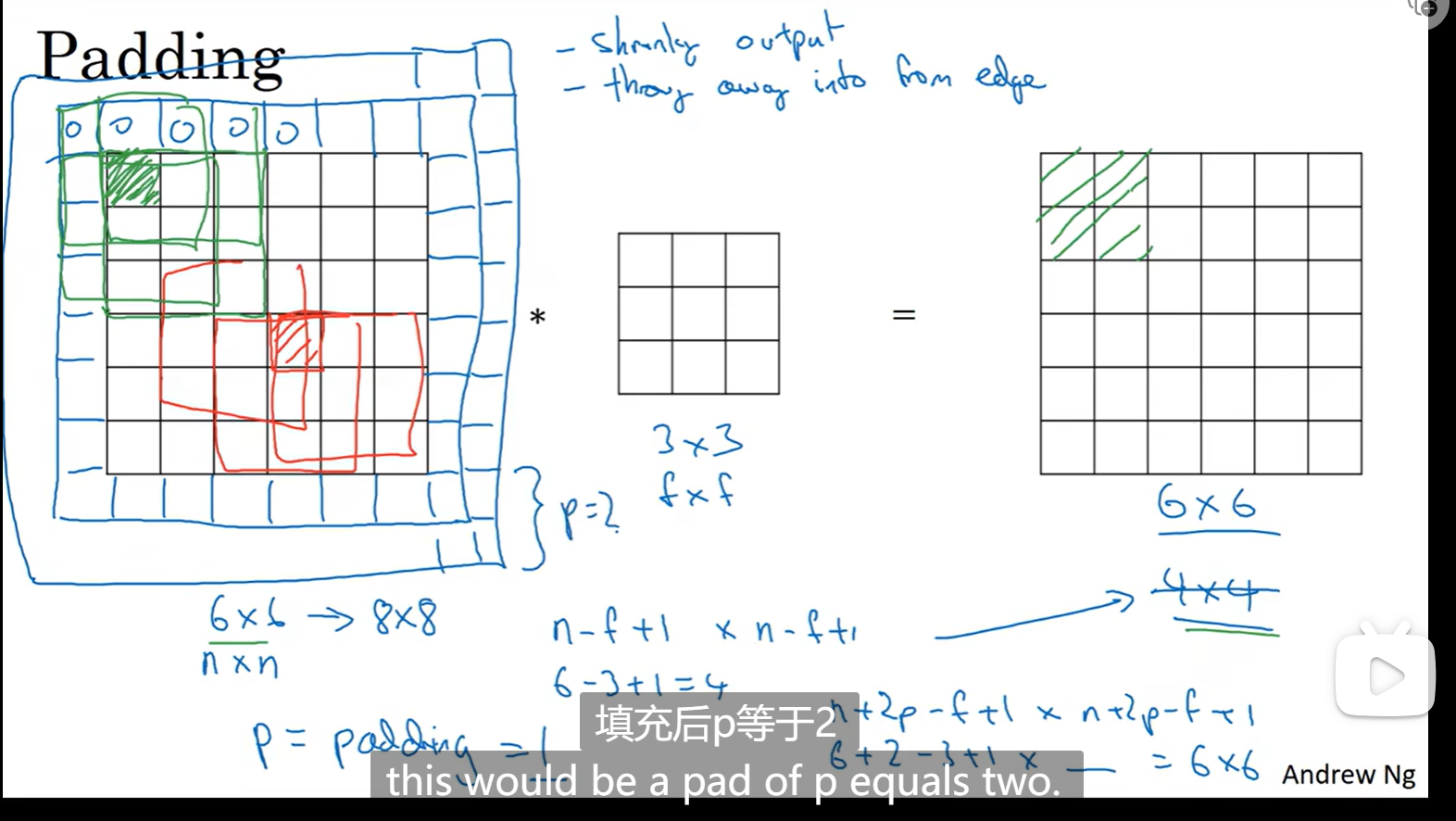
valid的是无padding,没有扩充，same是让输入和输出大小一致

image-20230711232927694

卷积步长

步长：过滤器每次和相符的矩阵进行计算，该矩阵移动方式为两步，计算出输出函数公式向下取整

image-20230712004337356

image-20230712083616130

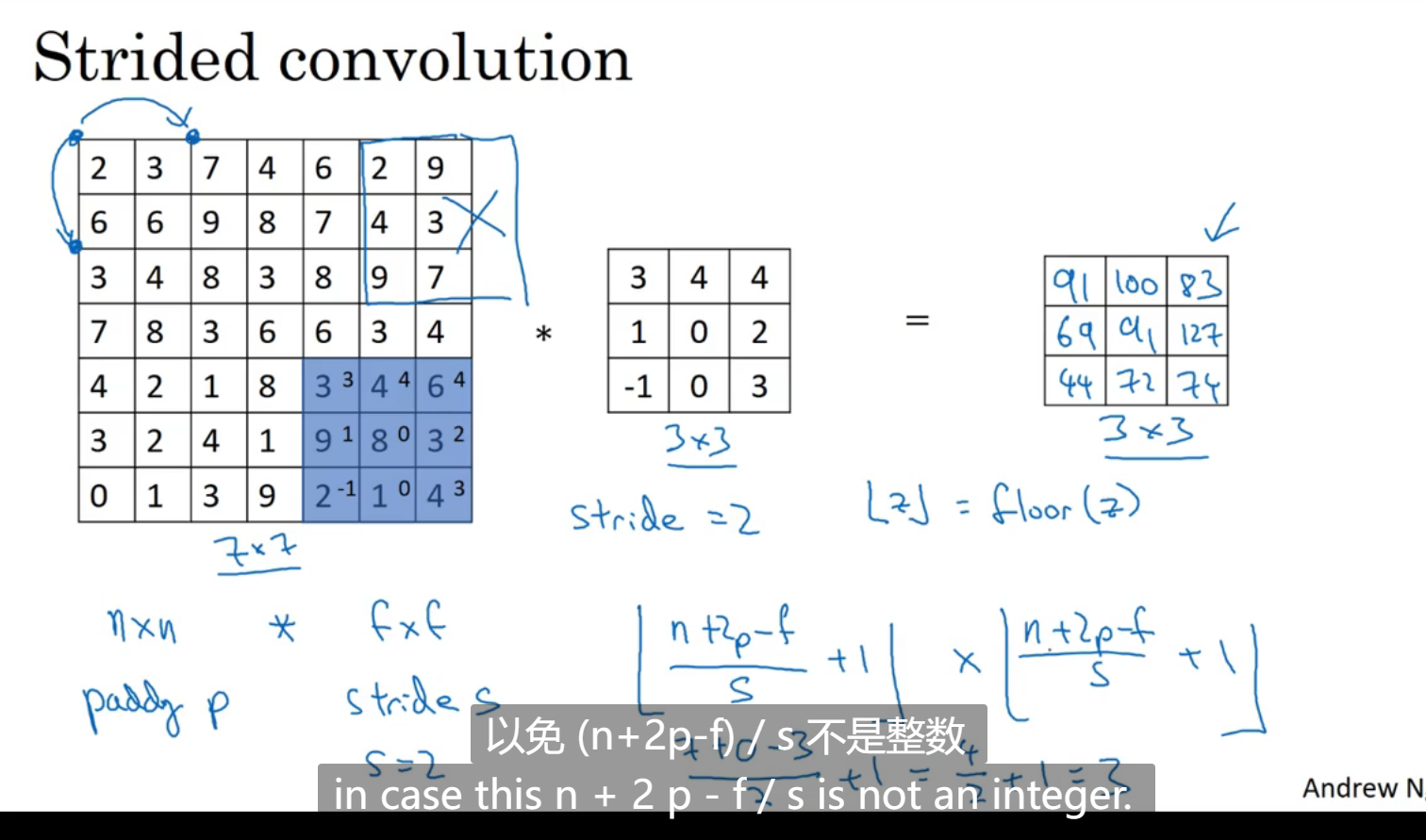
很多卷积定义是这样的：

image-20230712083518181

三维卷积

上一节是针对二维图像的卷积

针对三位卷积：将过滤器也定义成三维的(上面那一层是只对红色做垂直边缘检测，下面那一层是对所有颜色做边缘检测，输入图像的channel和过滤器的channel要一致，最后输出是一维的，用方块来做计算)：

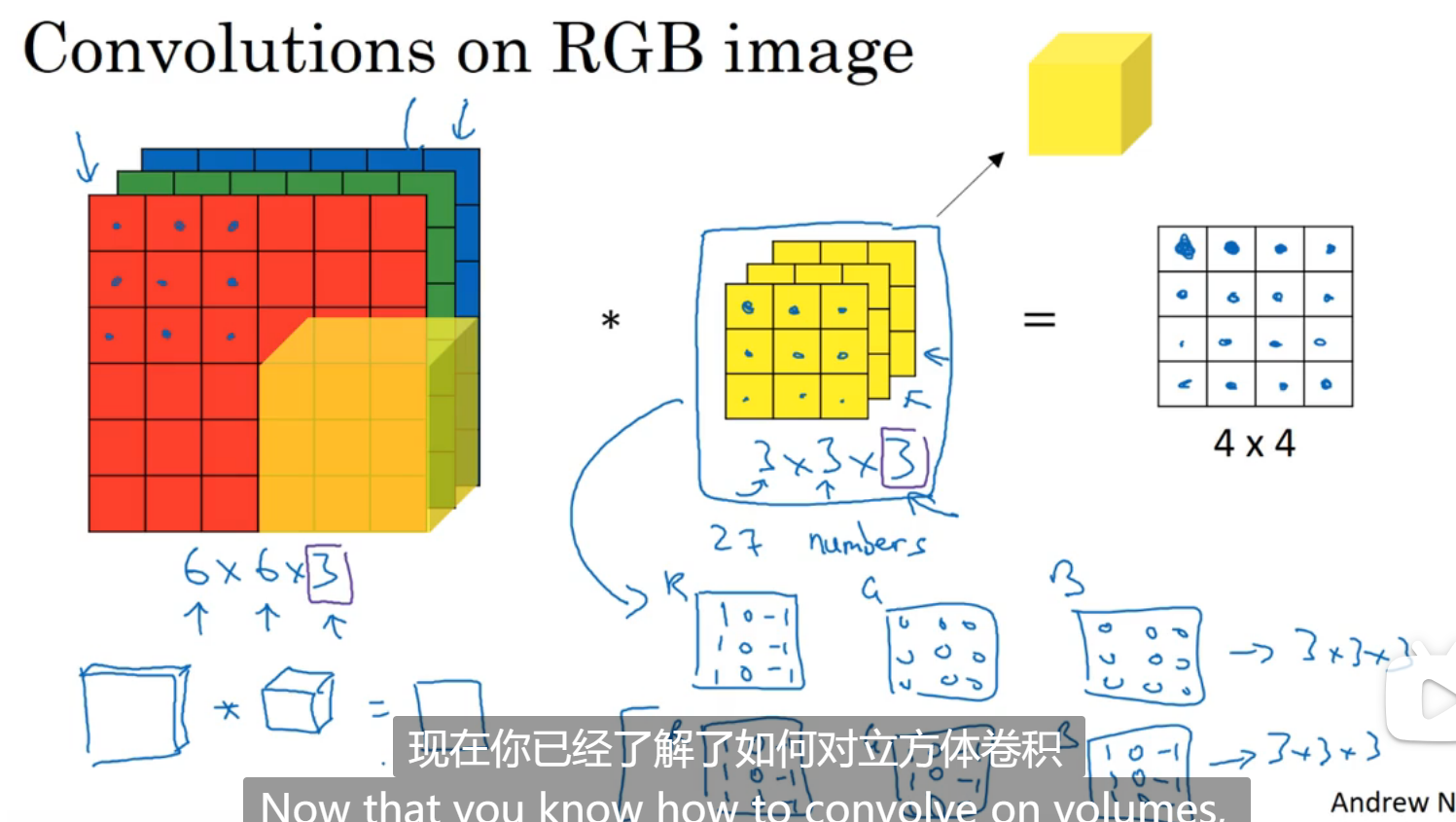
如果又要做垂直边缘检测又要做水平边缘检测，就做两层然后将他们结合起来

image-20230712084644273

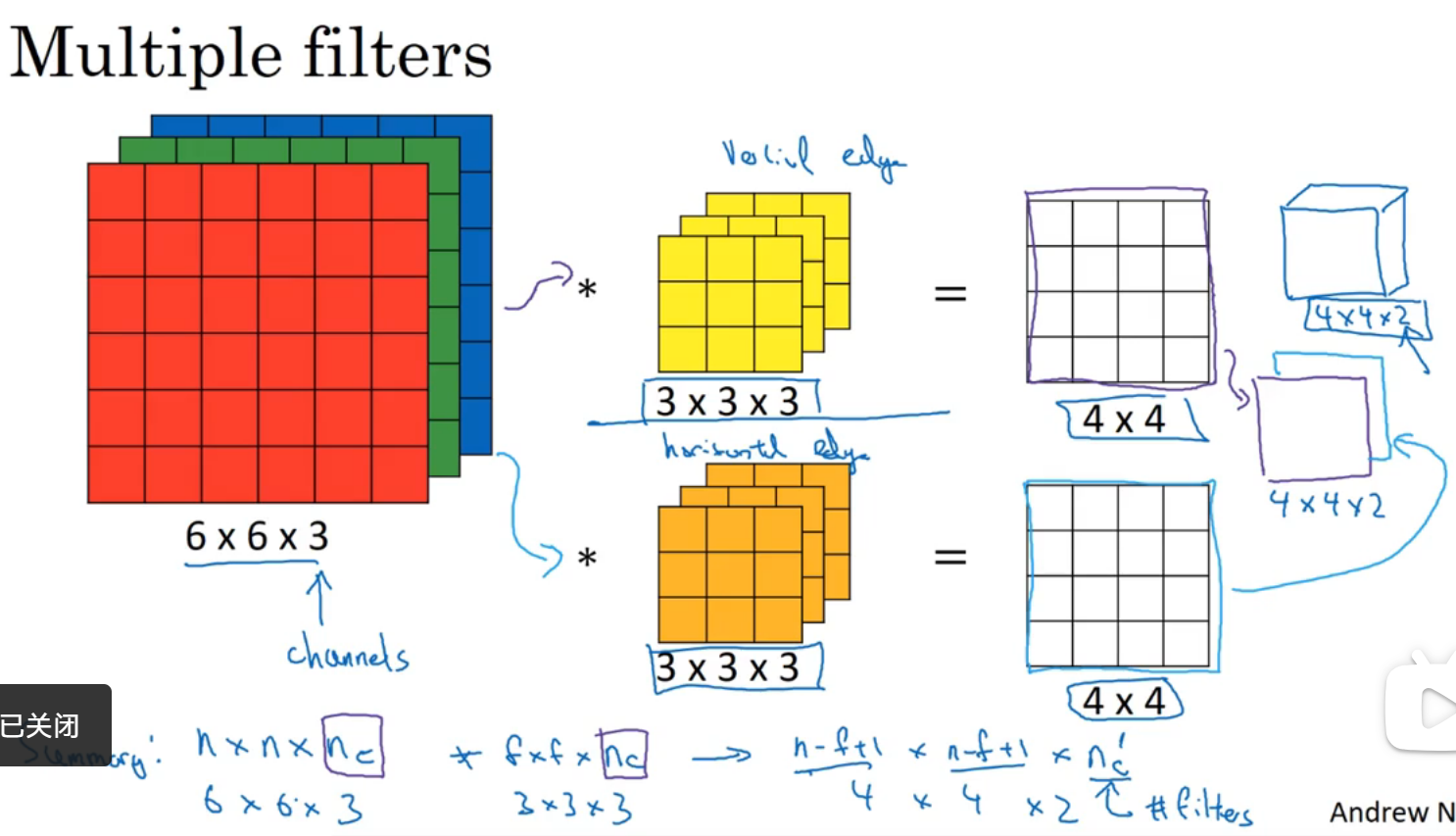
单层卷积网络：

用多少过滤器输出就有多少维度，下图展示了a[0]到a[1]的过程

image-20230712084955696

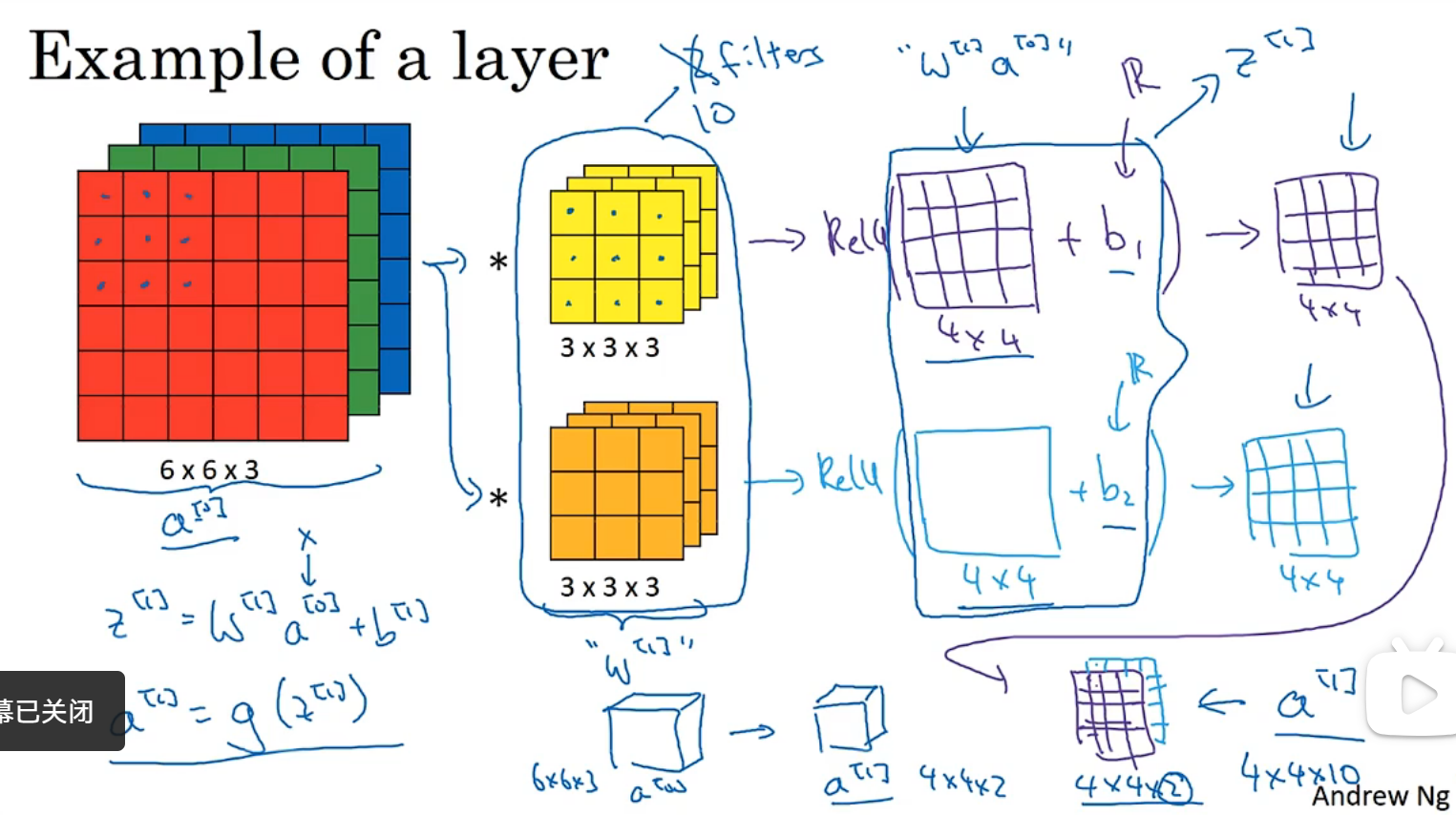
单层卷积网络（输出维度和过滤器数量一致，权重是过滤器乘以它的数量，权重的高宽是一致的，权重的channel和输入的channel是一致的）：

image-20230712085714334

简单卷积网络示例

趋势：高和宽不断变小，维度增大，最后将7 * 7 * 40的图像变成一个一维的，和前面三维图像变一维一致

image-20230712090822392

一个卷积网络往往分为三层（但是只用卷积也可能有很好的效果，池化层和全连接层比卷积层好实现）：

image-20230712091042761

池化层

最大池化（使用频率高）：如果在过滤器中提取到某个特征，那么保留其最大值，最大池化的效率也挺高：

image-20230712091346938

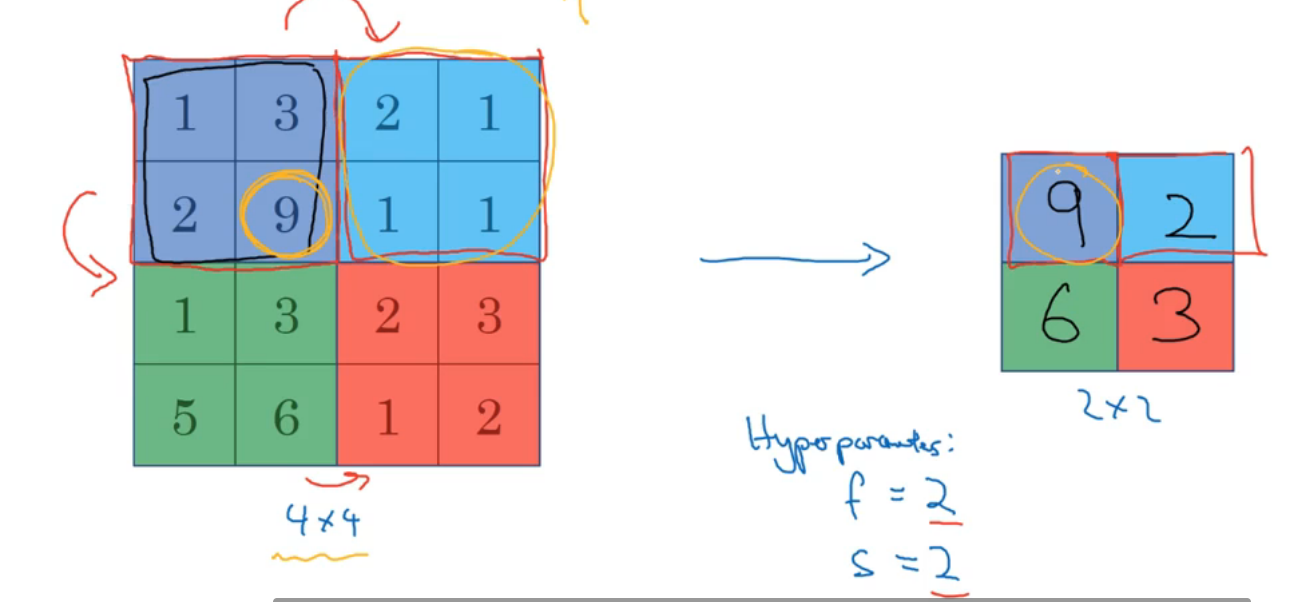
输入和输出维度一致

image-20230712091547489

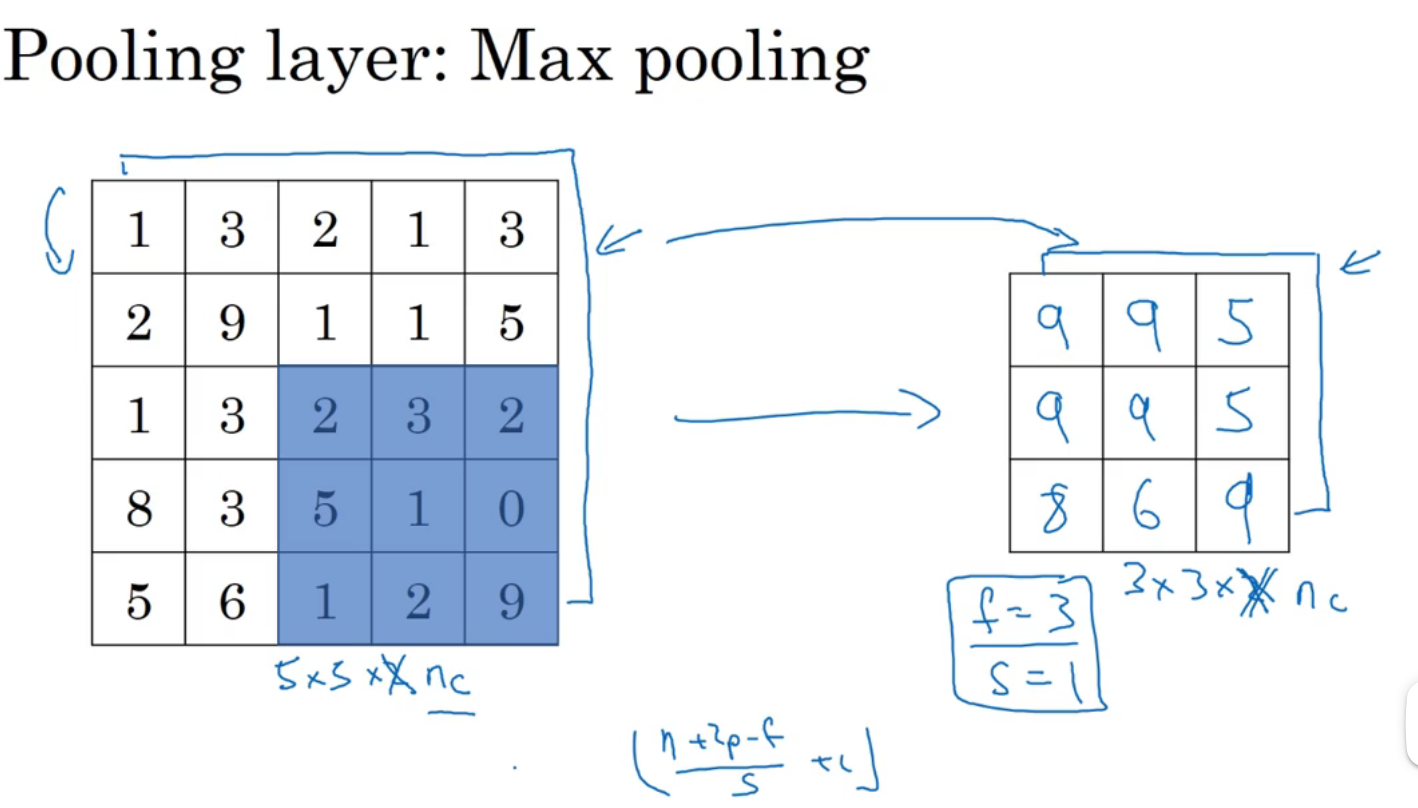
平均池化：取平均值

池化没有参数

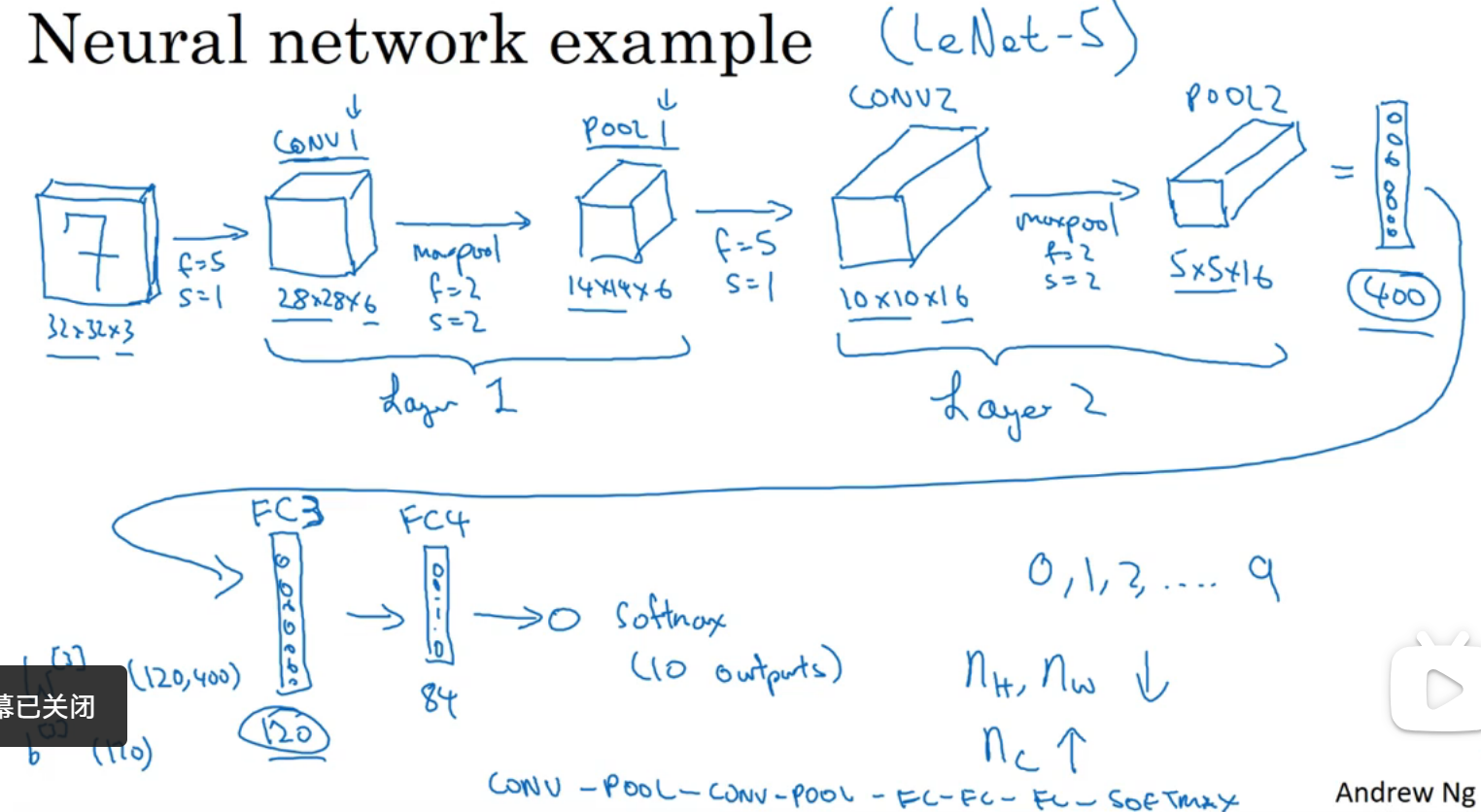
卷积神经网络示例

卷积神经网络常见状态：就如图像最下面所示，全连接和前面所讲的神经网络类似，一般是卷积层跟着池化层，由于池化层没有参数，所以池化层和卷积层很多时候称为一层

image-20230712092339751

image-20230712092630679

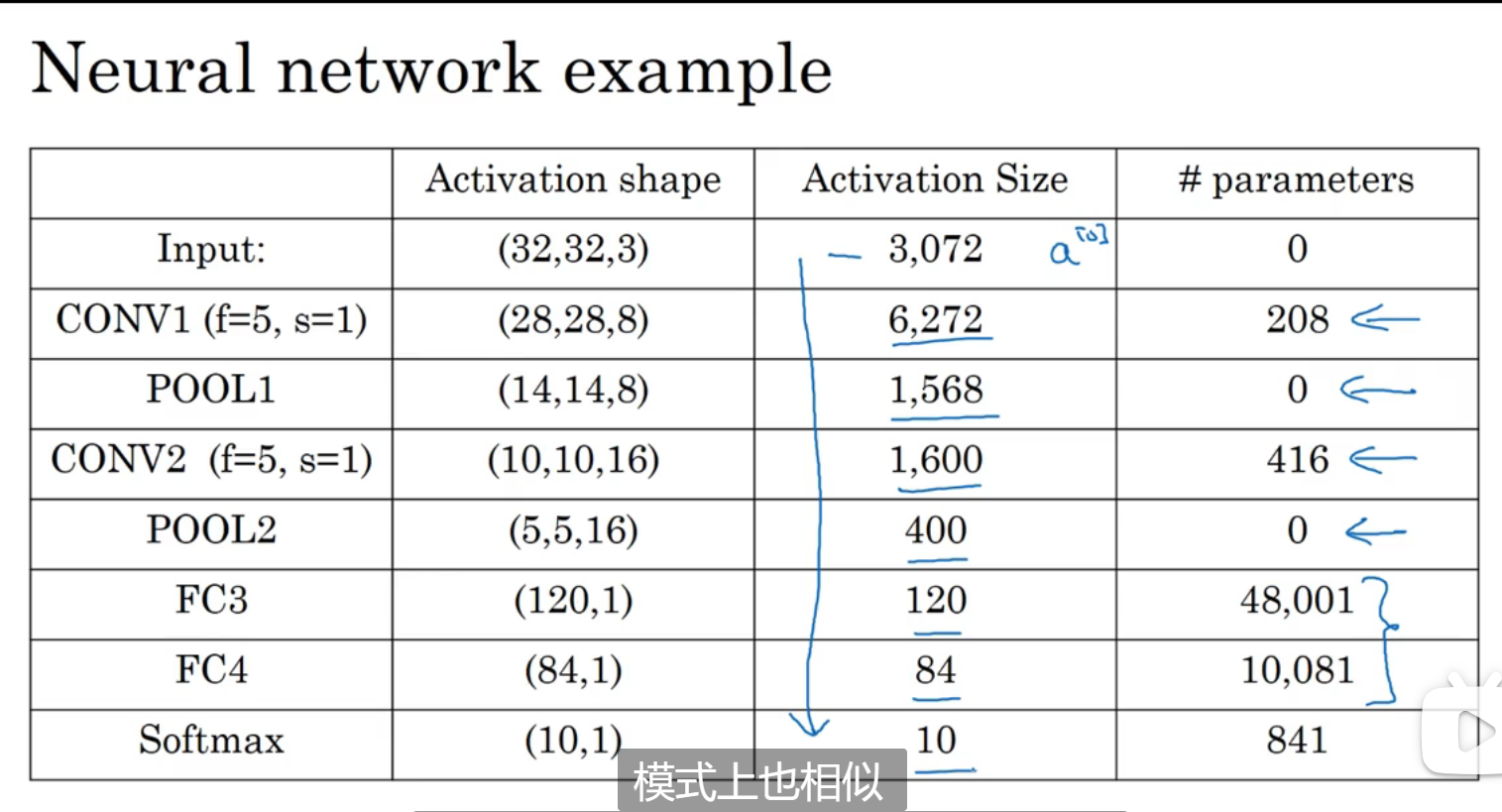
参数共享和稀疏连接

如果使用正常神经网络会出现参数过大的情况：

image-20230712093340375

卷积网络的输出每一个像素点只和一部分像素有关，避免过度拟合，并且改变输入的一些像素点只有对应的像素点会被改变