原创

Mini-batch梯度下降法

优化算法可以帮助我们快速训练模型

虽然向量化可以帮助我们提高运算速率，但是如果m很大，效率还是很低，因为我们每更新一次参数就需要重新进行正向传播，再更新参数，不断重复

现在选择算法使进行正向传播前先优化参数

可以把训练集分割成小一点的训练集，这些子集叫做mini-batch,如图所示，假设X有5000000个样本 将每1000个分成一个集合->x{i}

同时训练这些小的训练集

image-20230708162045308

伪代码(如果使用batch,要计算5000000个样本才迭代一次，但是如果使用mini-batch，每1000个样本就可以迭代一次参数)：

for i in range(1,5000):
    AL,cache=forward(X{i},Y{i},parameters)
    cost=compute_cost(AL,Y{i})
    grads=back_forward(parameters,cache)
    parameters=update_parameters(parameters,grads)

理解mini-batch梯度下降法

成本函数图像可能不再严格单调递减，但是总体趋势一定是递减的

image-20230708163120090

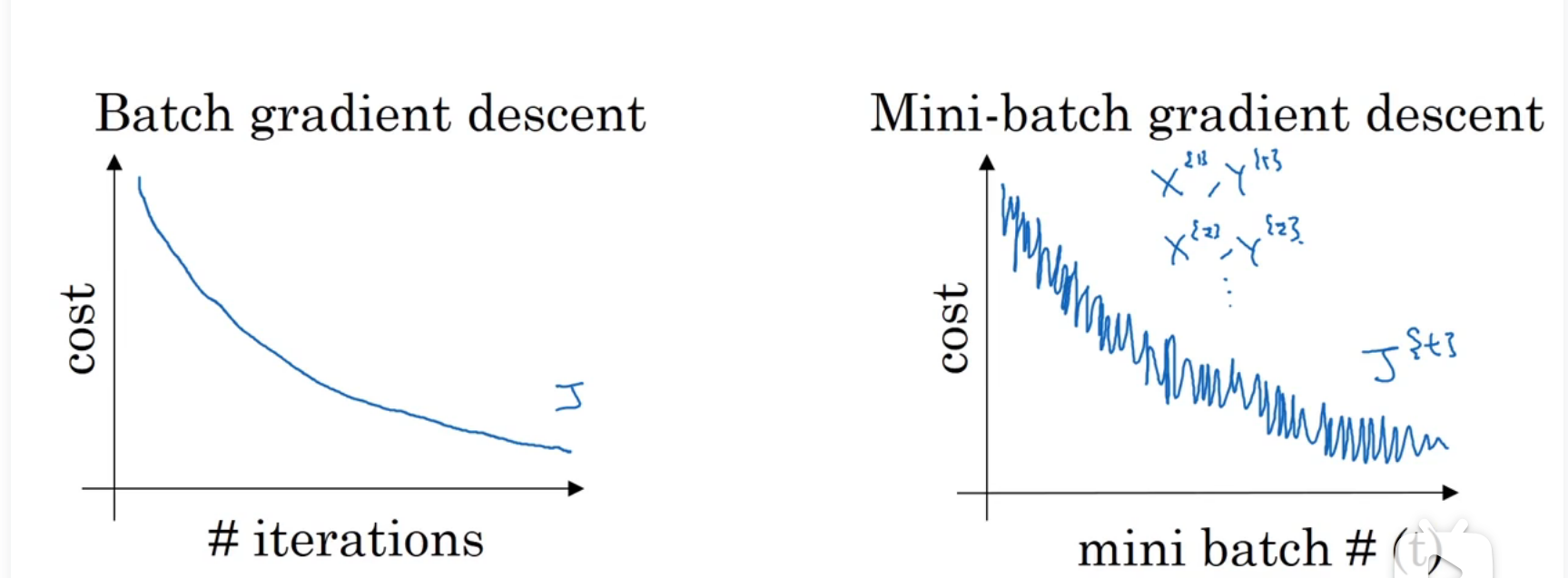
超参数：mini-batch的大小 如果mini-batch=m即代表就是batch,并未拆分 x{1},y{1}=x,y 每次迭代需要处理大量样本，耗时长

mini-batch=1:就有了新的算法，叫做随机梯度下降法，每个样本都互相独立，该种方法不可能有极小值，因为每个样本之间多少会有一定的差距，适合某一个样本的参数不一定就适合另一个样本，需要降低学习率

蓝色是m的迭代方向，紫色是1的迭代方向，绿色是采用mini-batch方法的迭代方向

image-20230708163703647

指数加权平均

eg:

image-20230708164540431

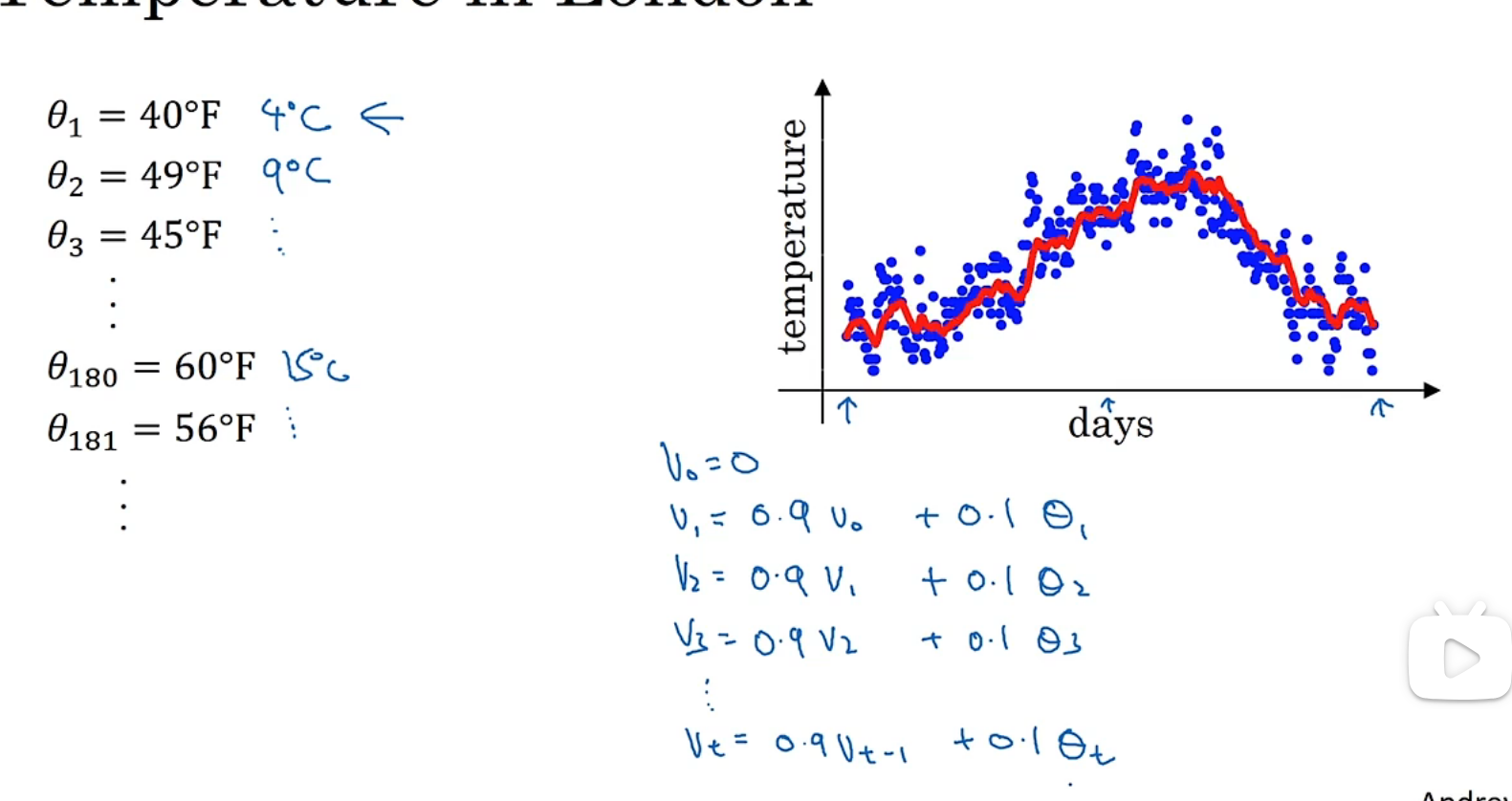
β越大，曲线越平缓：

image-20230708164854520

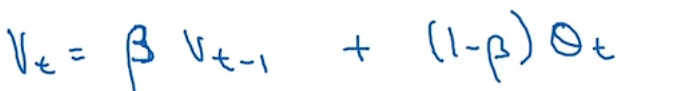
理解指数加权平均

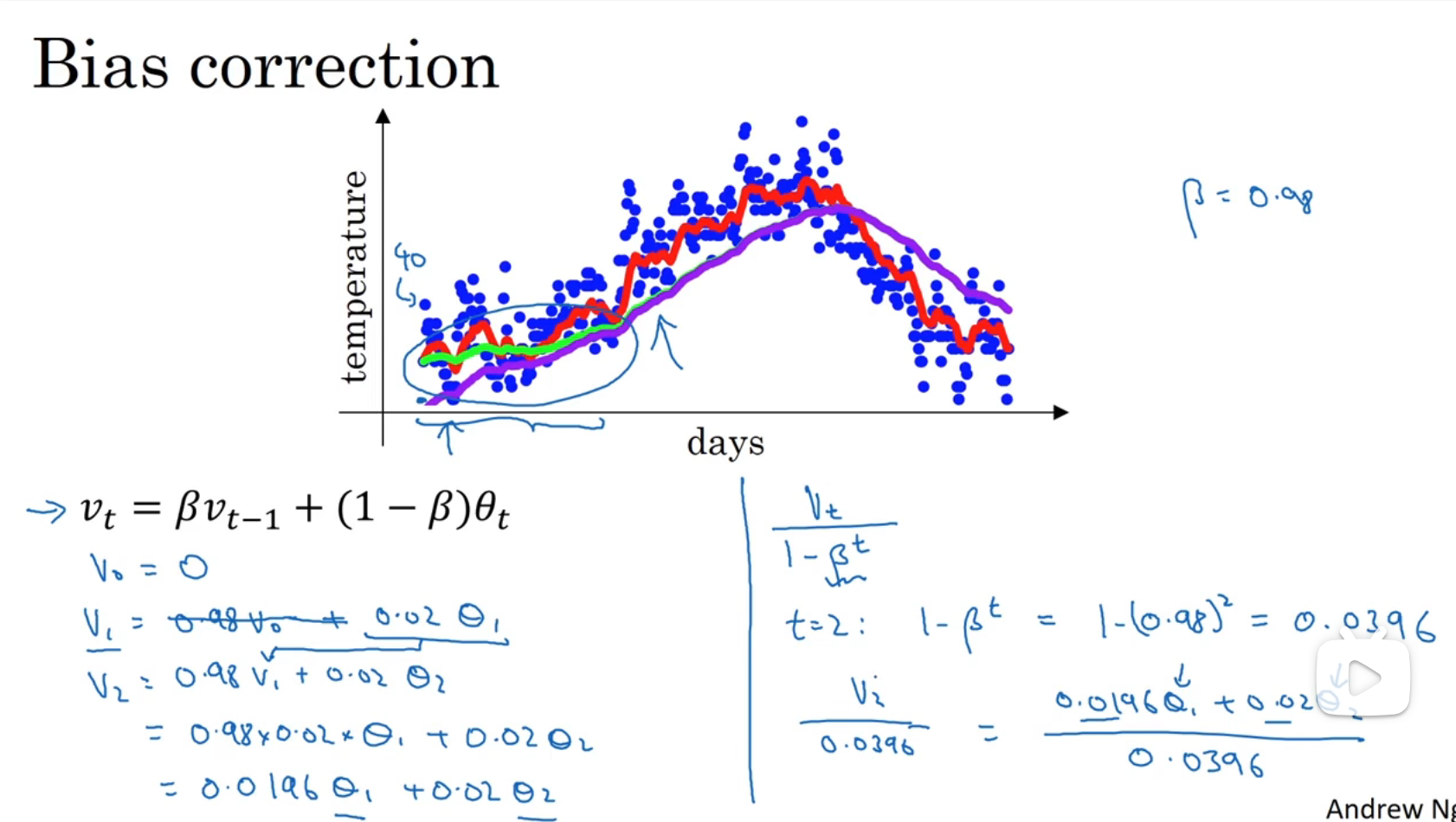
指数加权平均的指数修正

实际上我们得到的图形是紫线，因为设置初始值为0，v1=0.02θ1，很小，为了修正这种偏差，令除了Vi=0.98V(i-1)+0.02θi之外，再除以1-β^{t，随着t越来越大，1-β}t越来越接近于1，紫线和绿线越来越接近

image-20230708190504966

动量梯度下降法

Momentum梯度下降法：计算梯度的指数加权平均数，并利用该梯度更新权重

成本函数理想要求：学习率不宜过高，不然波幅就会很大，同时也希望学习时间够快

得到dw的移动平均数，这样可以减缓梯度下降的幅度，因为如下图，可能发现成本函数接近极小值的图象是纵轴上的摆动平均值接近于0，最终纵轴摆动变小了，学习速度变快

image-20230708192134734

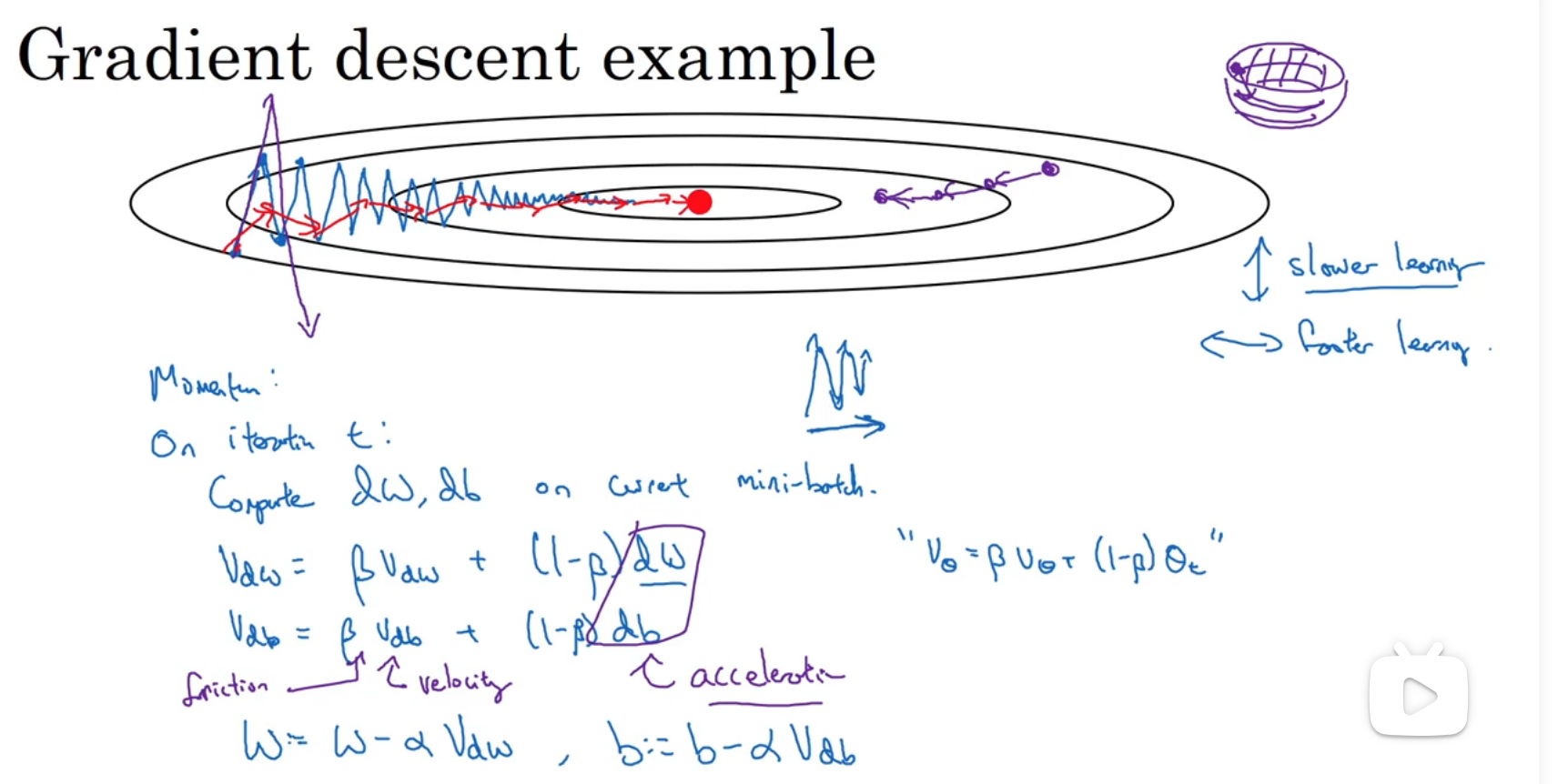
现在有超参数α和β，β控制着指数加权平均数，最常用的值是0.9，相当于平均了前十次的导数

两个初始值都是0(紫色部分也是一种，但是不怎么用)

image-20230708192425356

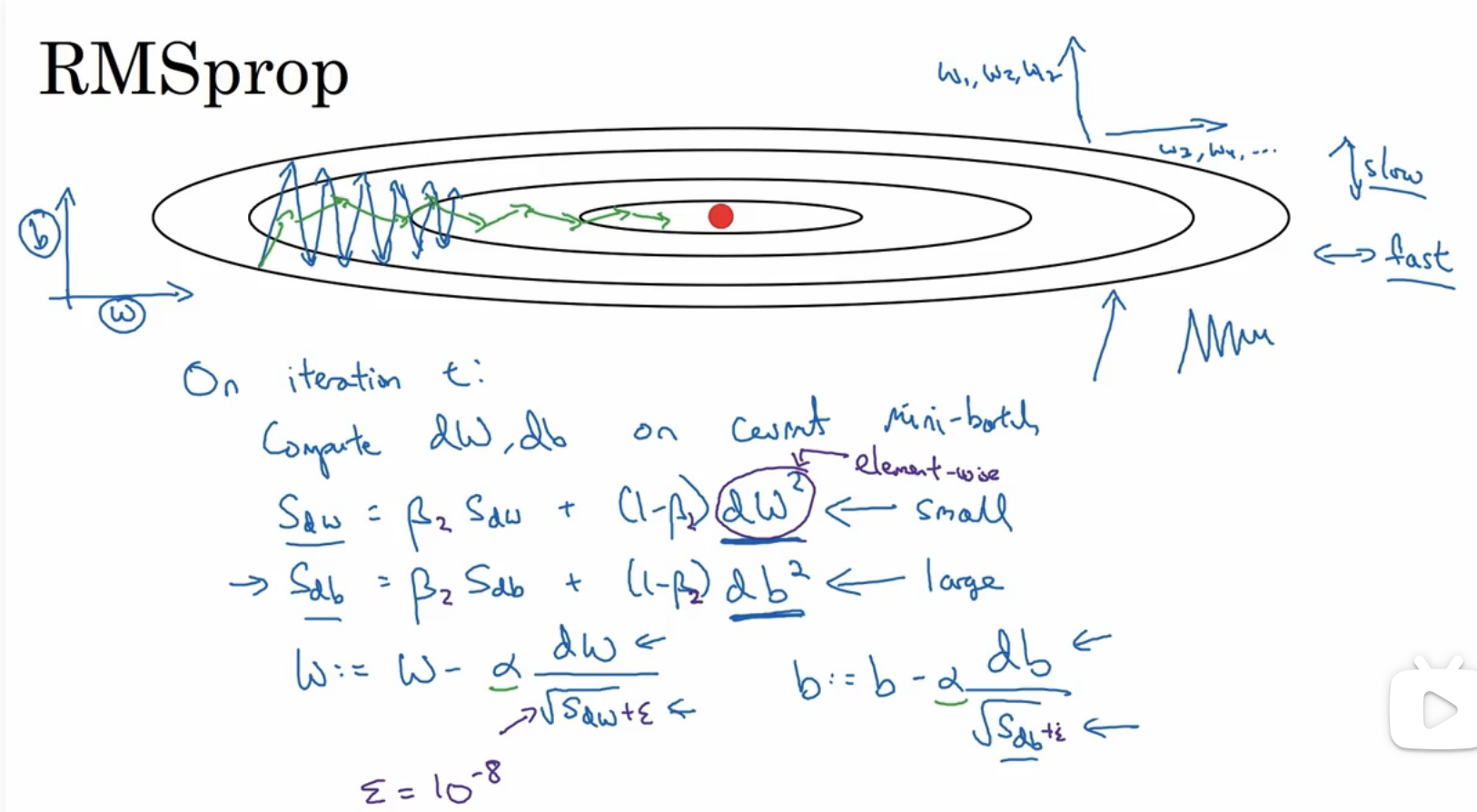
RMSprop

root mean square prop

该算法也可以加快梯度下降

这里b表示纵轴，w表示横轴，现在希望b变化幅度不要太大，加快w的变化

db会比较大，从而导致Sdb也比较大，dw会比较小，从而导致Sdw也比较小，从而使b变化幅度不会太大，w变化幅度也不会太小，从蓝色图像变成绿色图像，同时可以用更大的学习率加快学习，一般为了防止根号下的内容过于小，会加上一个很小的值

image-20230708193531517

Adam优化算法

adaptive moment estimation

将RMSprop和动量梯度下降法结合起来

image-20230708194139616

参数设置，学习率需要不断调试选出最合适的

image-20230708194741374

学习率衰减

比如使用mini-batch时，成本函数在迭代过程中会有波幅，但都是下降朝向最小值，会不断精确的收敛，但是不会真正的收敛，因为用的α是固定值

所以α应该在前期是比较大的，然后随着不断学习，要做到精确收敛，α要不断变小

decay-rate是衰减率，epoch-num是次数

image-20230708201502202

α的其他衰减函数

局部最优的问题