原创

神经网络概论

引入层的概念，x(i)表示第i个样本 w[1]表示第一层的w，表示是在第一层用到的w

上一节学到的模型如下：

image-20230630222739969

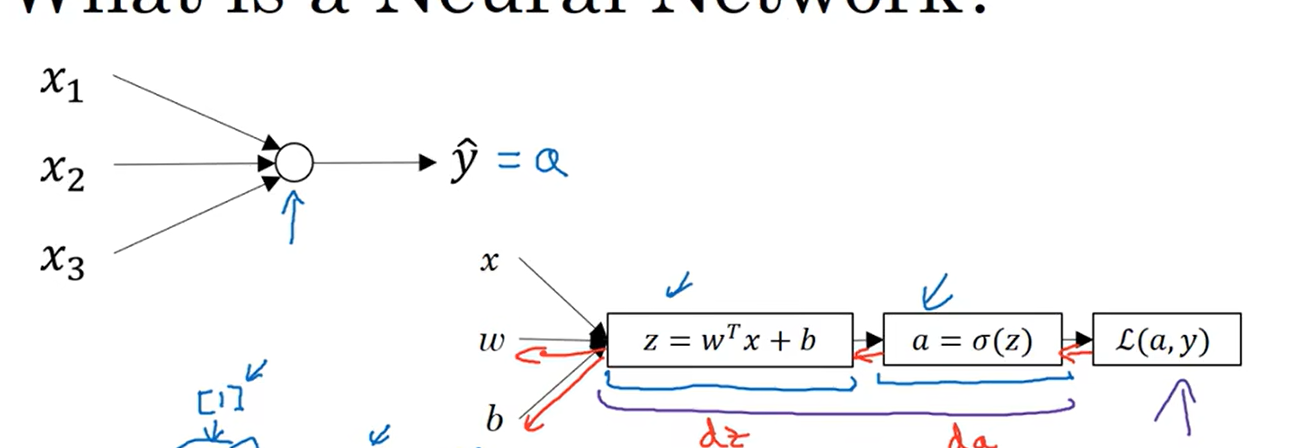
扩展：

image-20230630222752919

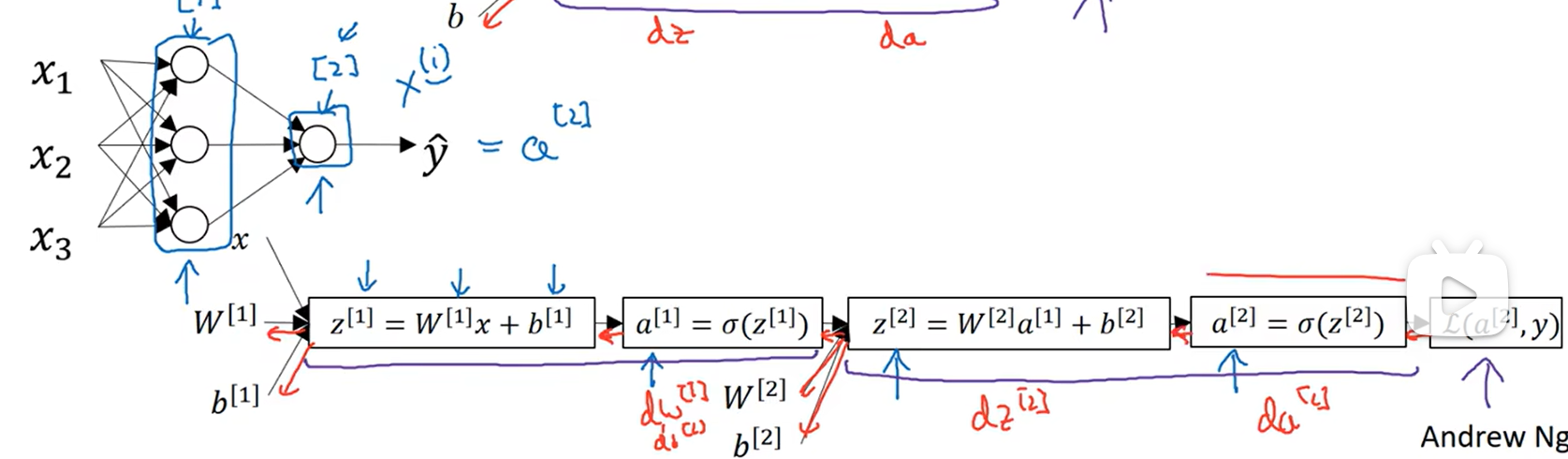
和上面的图一样，算出a[1],但是会继续算，继续根据参数计算z[2],最后得到损失函数(交叉熵损失)

神经网络表示

隐藏层：在训练集中，这些中间节点的真实数据，但是在训练集中是看不见的，只能看到输入输出

下图是双层神经网络示例：是双层不是三层是因为输入层通常不被看作一个层，第零层

从左到右依次是输入层，隐藏层，输出层

image-20230630223343705

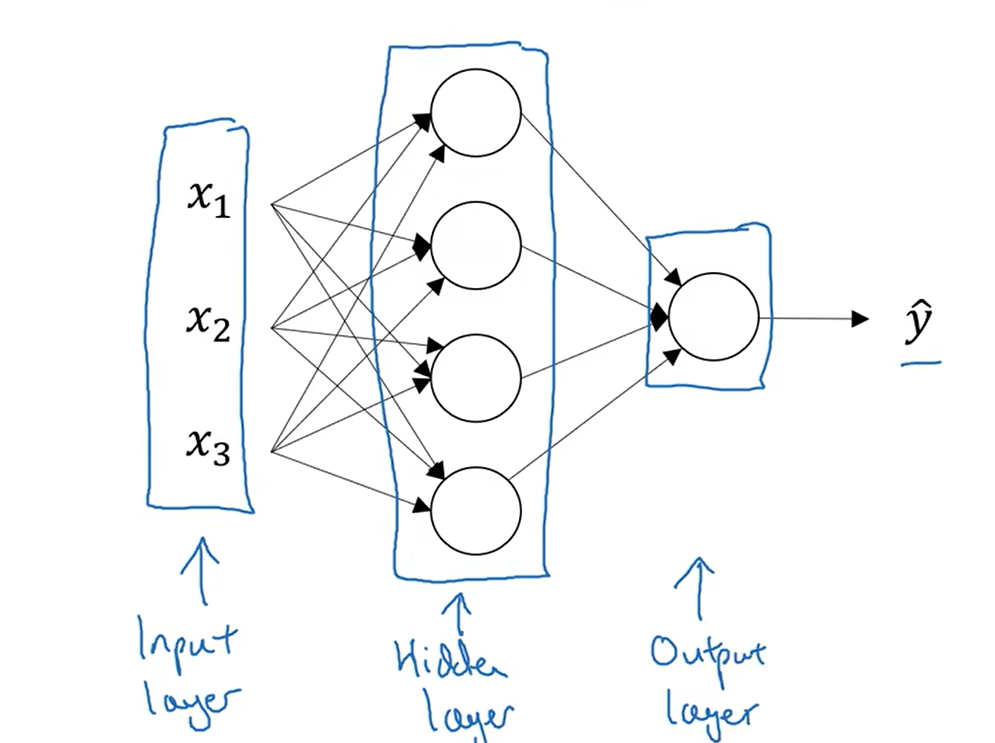
X:输入特征，或者用a[0]表示，这里的0代表第0层，就是输入层，输入层将X/a[0]传给隐藏层，隐藏层产生a[1],在上图中a[1]应该是一个41的矩阵，最后的y_hat=a[2]，隐藏层可能有两个相关参数w[1],b[1],这里的w应该是3 4的矩阵，b是4 * 1矩阵，4代表这里有四个输出，即a[1]是一个4 * 1的矩阵，3代表x的输入特征数，输出层有两个相关参数w[2],b[2],

计算神经网络的输出

如图所示，双层神经网络logistic函数

image-20230704175622967

image-20230704184159224

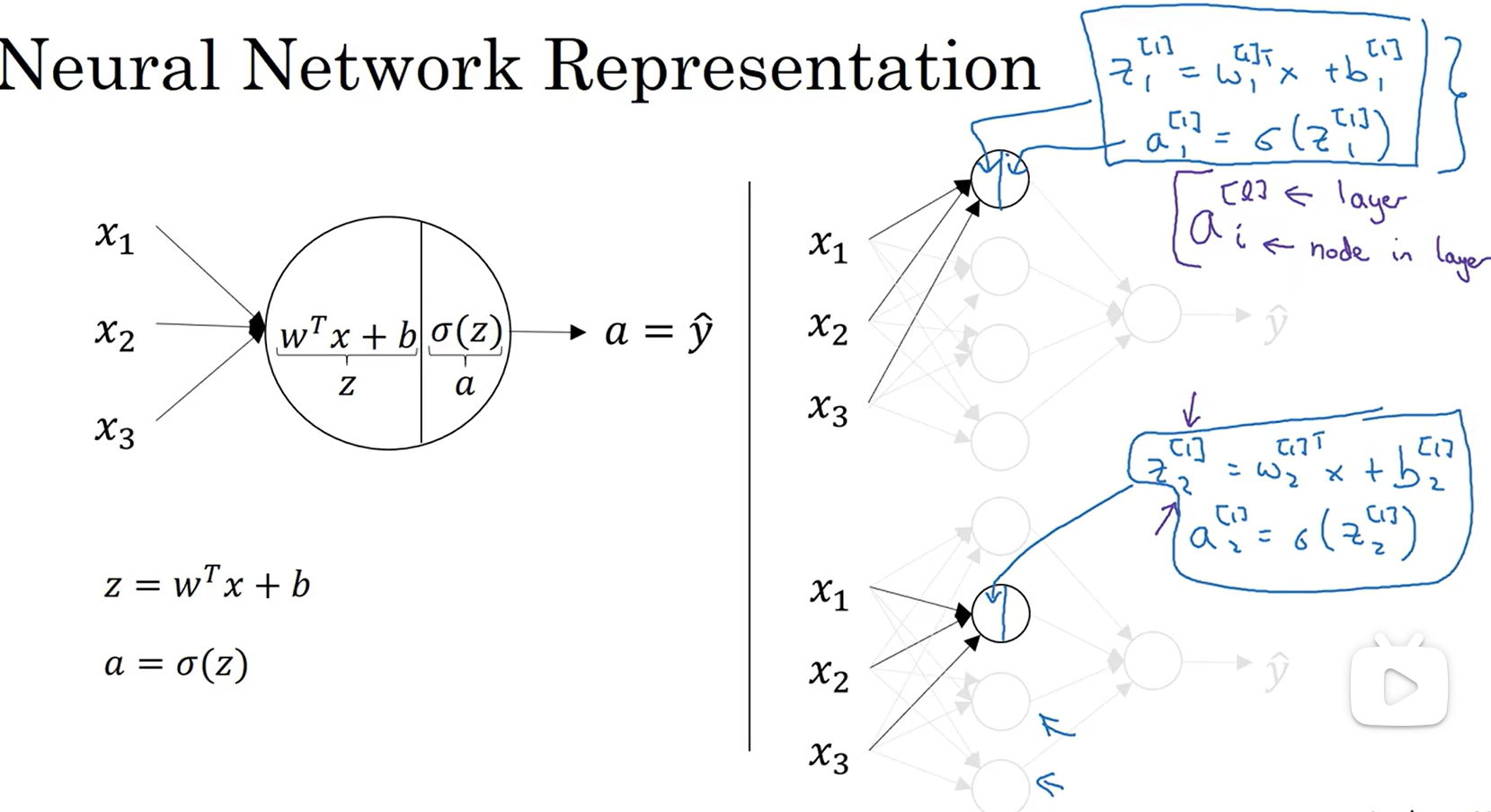
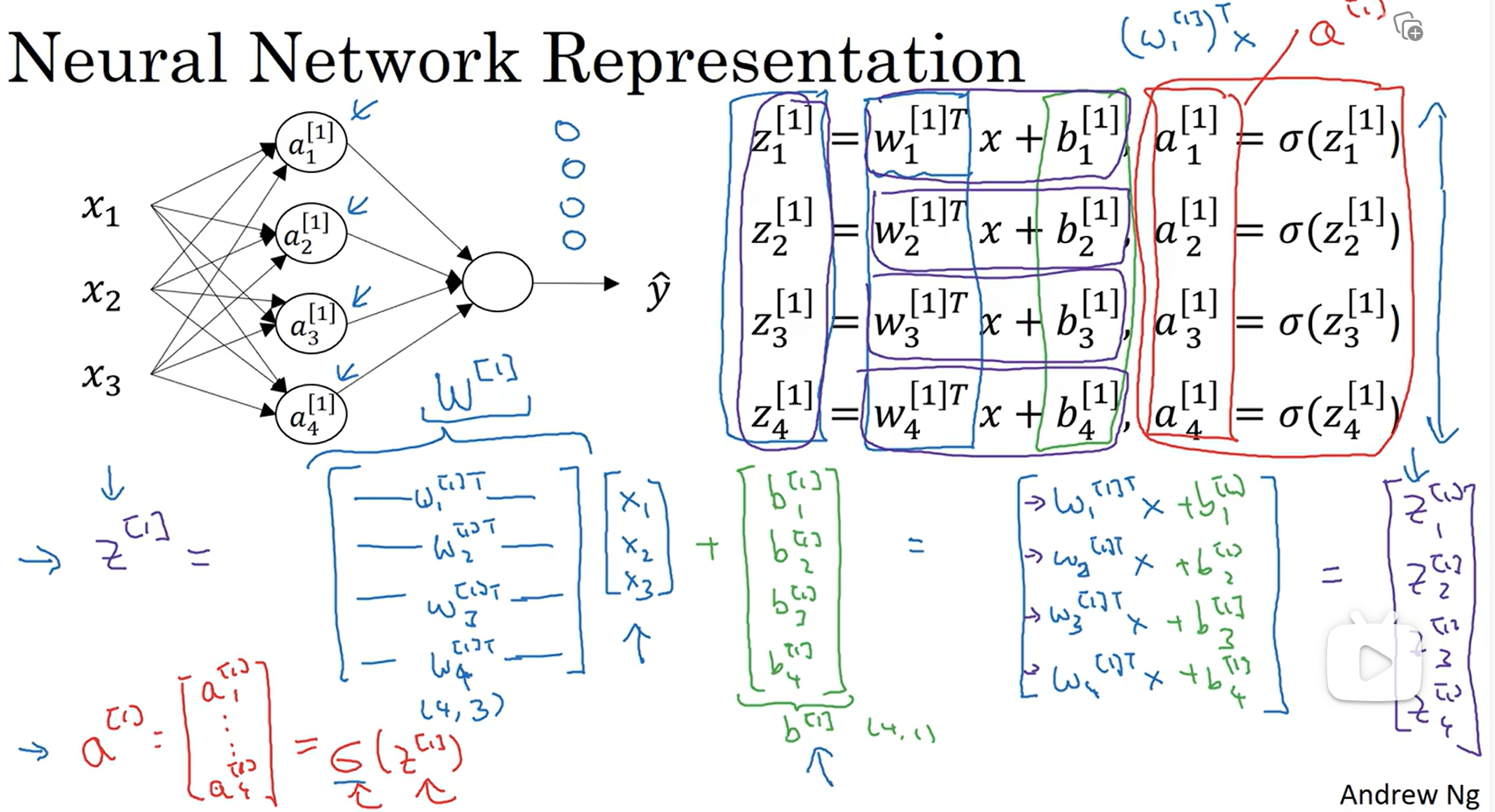
如图所示，这里将一层的w列为了一个矩阵，每一层的每个w都是nx * 1矩阵，和x是一样的，上图中第一层有四个结点，就用了四个w，将四个w排成一个矩阵，也就是nx * 4矩阵，然后将这个排列好的矩阵转置，变成上图所示的形状，再乘上x，再加上b，将第一层的b也设为一个矩阵，将上图总结：

image-20230704184843687

伪代码如下(m个样本):

for i in range(1,m):
    z[1](i)=W[1] * x(i) + b[1]
    a[1](i)=sigmoid(z[1](i))
    z[2](i)=W[2] * x(i) + b[2]
    a[2](i)=sigmoid(z[2](i))

改进方法：将m个样本合并到一个矩阵,X是nx * m矩阵，W[i]是q * nx矩阵，q是第一层结点的数量，W[i] * X是q * m矩阵，一列表示一个样本，到最后也是，一列表示一个样本

Z[1]=W[1] * X + b[1]

A[1]=sigmoid(Z[1])

Z[2]=W[2] * X + b[2]

A[2]=sigmoid(Z[2])

向量化实现的解释

激活函数(sigmoid)可以有更多选择

激活函数

g()用更多的选择，不止sigmoid()函数

比如用tanh(z)代替sigmoid(),前者的函数：e^z-e(-z)/e^z+e(-z) 后者的函数：1/1+e^(-z),前者是后者的平移，且平均值为0如图所示：

image-20230704203251929

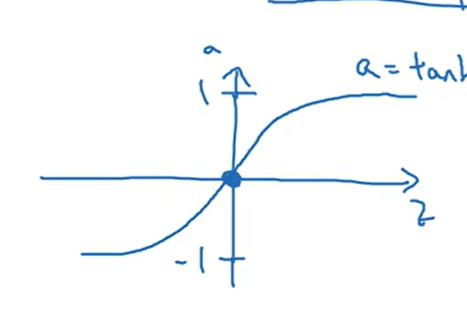
当要二元分类的时候，也就是y是0/1时，用sigmoid更方便，但是在前面几层可以tanh函数

sigmoid和tanh函数的缺点，当z很大的时候，斜率很低

RelU(修正线性函数)函数：a=max(0,z),如图

image-20230704203606547

选择激活函数的方法：

• 如果要求二元分类，选择sigmoid,然后其他单元都选择ReLU，ReLU运算的速度会比其他的快很多
• 有时候也用tanh

另一种ReLu函数：泄露的ReLU(leaky RelU),也就是当z小于0时，斜率不再是0，而是一个很小的数字 a=max(0.01 * z,z)

总结：

• sigmoid只用于二元分类，tanh会更优越
• ReLU在不知道用什么激活函数的时候使用

为什么需要非线性激活函数

如果让g(z)=z(恒等激活函数,一种线性激活函数方式)有什么后果

A[1]=W[1] * X +b[1]

A[2]=W[2] * A[1] + b[2]=W[2] * (W[1] * X + b[1]) + b[2]=W[1] * W[2].T * x + W[2] * b[1] + b[2]

还是W[] * X + b[]形式

通常只有输出层才能用线性激活方式

激活函数的导数

• sigmoid函数导数：前面计算过一次，a=1/(1+e^(-z)),da/dz=a(1-a)

• tanh函数导数：

image-20230704212033011

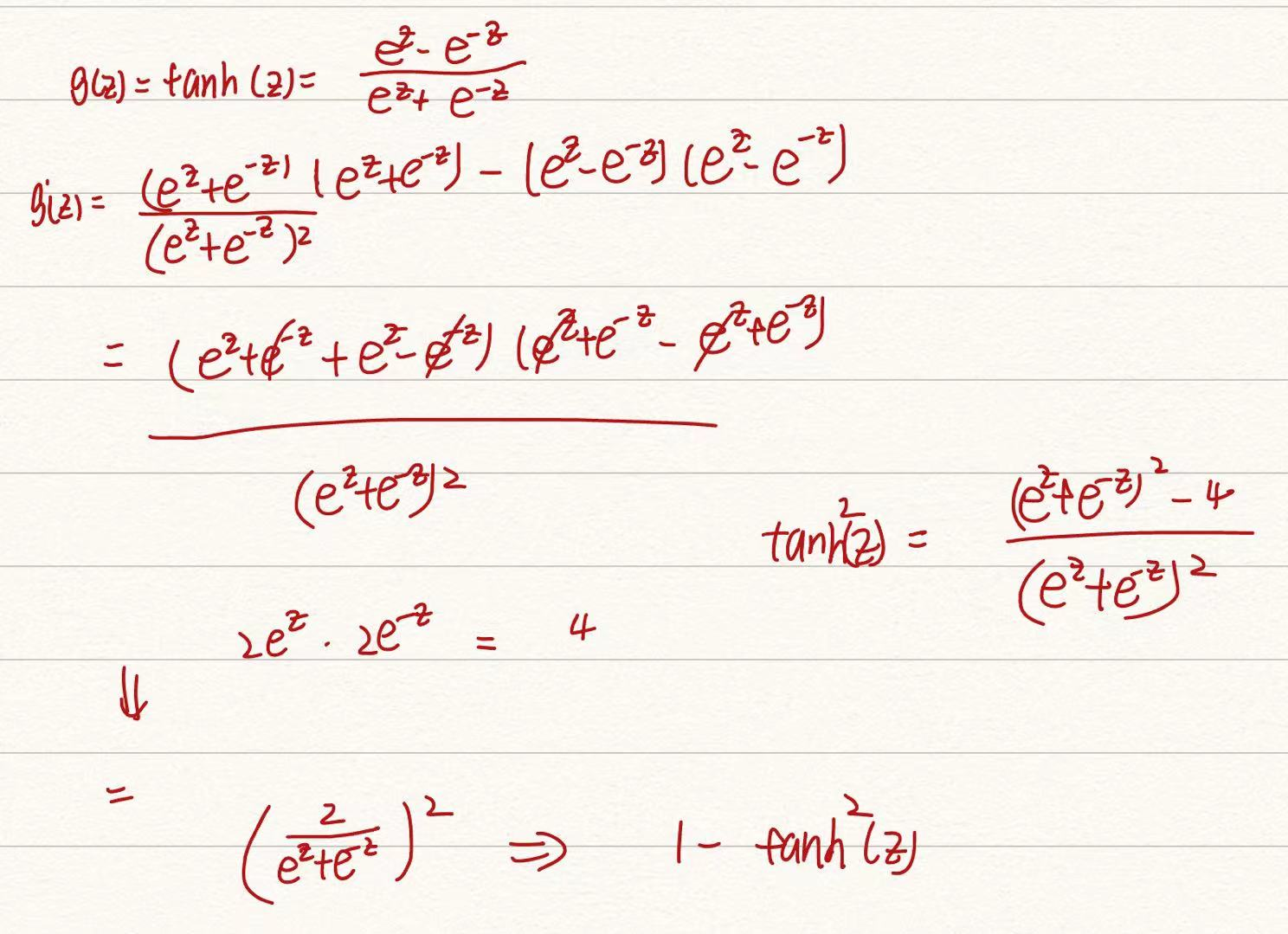
• ReLU函数：max(0,z),导数比较好计算，但是z等于0的导数需要自己定义

• 泄露的ReLU函数：max(0.01 * z,z),同样，z=0是需要自己定义的：

  

  image-20230704212427680

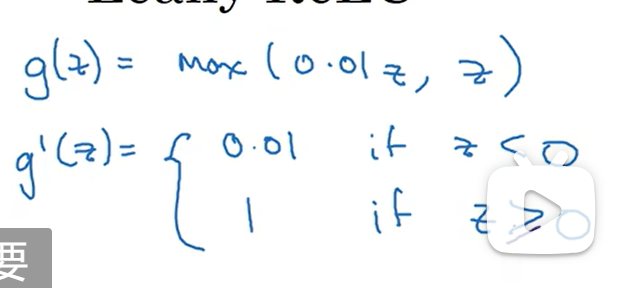
神经网络的梯度下降法

单层隐藏神经网络的反向传播：

参数设置：W[1] b[1] W[2] b[2],n[0]表示多输入特征，n[1]表示隐藏单元，n[2]表示输出单元(前面讲的情形中n[2]是1)

W[1]是n[1] * n[0],b[1]是n[1] * 1,W[2]是n[2] * n[1],b[2]是n[2] * 1

成本函数(cost function):J(W[1],b[1],W[2],b[2])=Σ(L(y_hat,y))/m,在该情形中，y_hat是a[2]

初始化参数对于梯度下降法很重要：

repeat: dw[1]=dJ/dw[1],dw[2]=dJ/dw[2],db[1]=dJ/db[1],db[2]=dJ/db[2],w[1]=w[1]-α * dw[1]……

image-20230704215112255

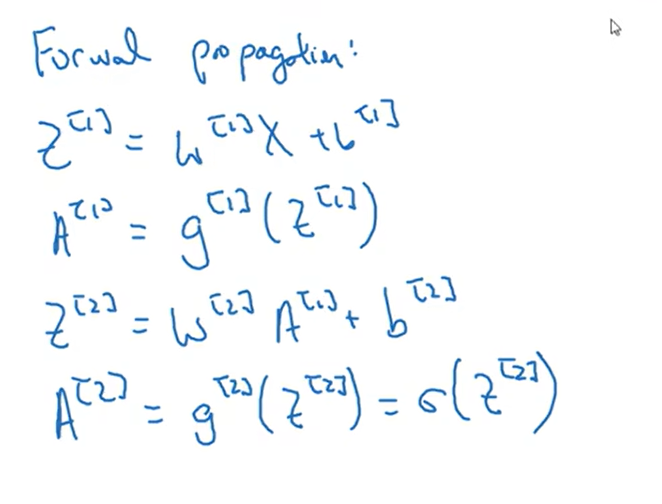
由前面的计算得,dz[1]的乘法是相同维度的矩阵对应位置元素相乘

image-20230704215936385

随机初始化

不能直接讲W1/W2都定义成zero矩阵，这样对于隐藏节点没有意义，以为相当于是用相同的方法进行计算

因此选择用随机初始化：

W1=np.random.randn(n_h,n_x)*0.01
b1=np.zero((n_h,1))