原创

用(x,y)表示一个单独的样本，x是n维的一组向量，y标签值为0或者1

训练集由m个训练样本组成：(x1, y1) (x2, y2) (x3, y3)...(xm, ym)

x=[x1,x2,x3...xm]->n*m

y=[y1,y2,y3...ym]->1*m

训练集m_train 测试集m_test

logistic回归

针对输出标签y是0/1时(二元分类)

eg:判断一张图片是不是猫 y=p(y=1|x) 0<=y<=1

输入：x->n * m w->n * m b->R

输出：y

若用线性回归方程：y=w(T) * x+b 无法确保y的范围 solution: use sigmoid(Z)函数——>y=sigmoid(w^T * x+b),sigmoid为激活函数，通过该方法，b和w才是需要学习找到的参数

image-20230628205550177

image-20230628205903577

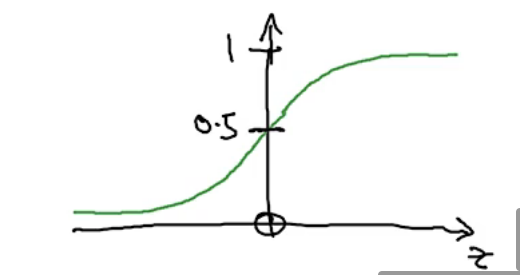
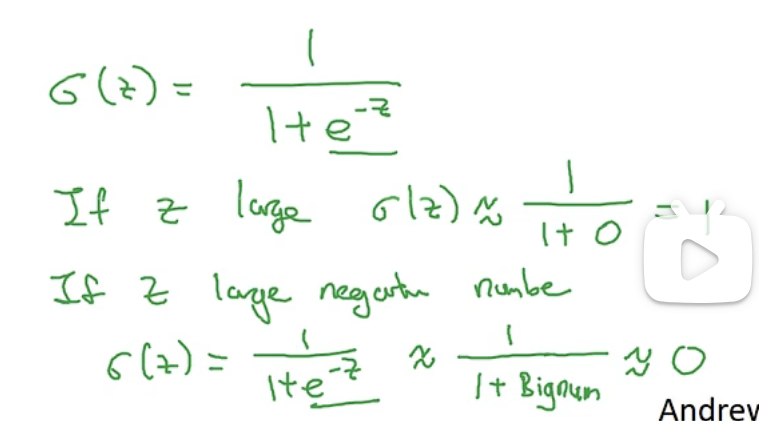
logistic回归损失函数

为了训练w,b需要定义一个成本函数(cost function)

令z(i)=w^T*x(i)+b

loss(error) function:

• 训练出的y和实际的y的差，或者是他们差平方的二分之一(但是这样不适用于梯度下降法)

  

  image-20230628210813246

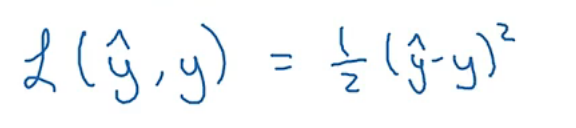
• 逻辑回归实际使用的损失函数：

• 损失函数是针对单个训练样本，是衡量在单个训练样本上的表现

cost function:

• 衡量在全体训练样本的表现
• 成本函数：J(w,b)=1/m*ΣL(y(hat)，y)->损失函数求和求平均值

梯度下降法(gradient decent algorithm)

用梯度下降法训练w和b，即找到令成本函数J(w,b)最小的w,b

image-20230628212108282

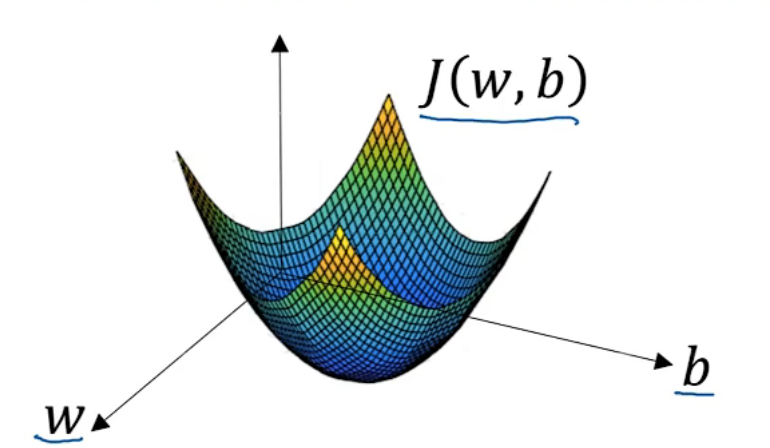
针对这种凹图形，首先找到任意的w,b初始化，梯度下降法就是从初始点开始，朝最陡的下坡方向走一步，是梯度下降的不断迭代，到最后收敛到全局最优解

eg:α是学习率，学习率可以控制每一次迭代(步长)，比如如果该点的导数小于零，w就增加，如果该点的导数大于零，w就减小，在该图中为了方便省去了b

image-20230628213522865

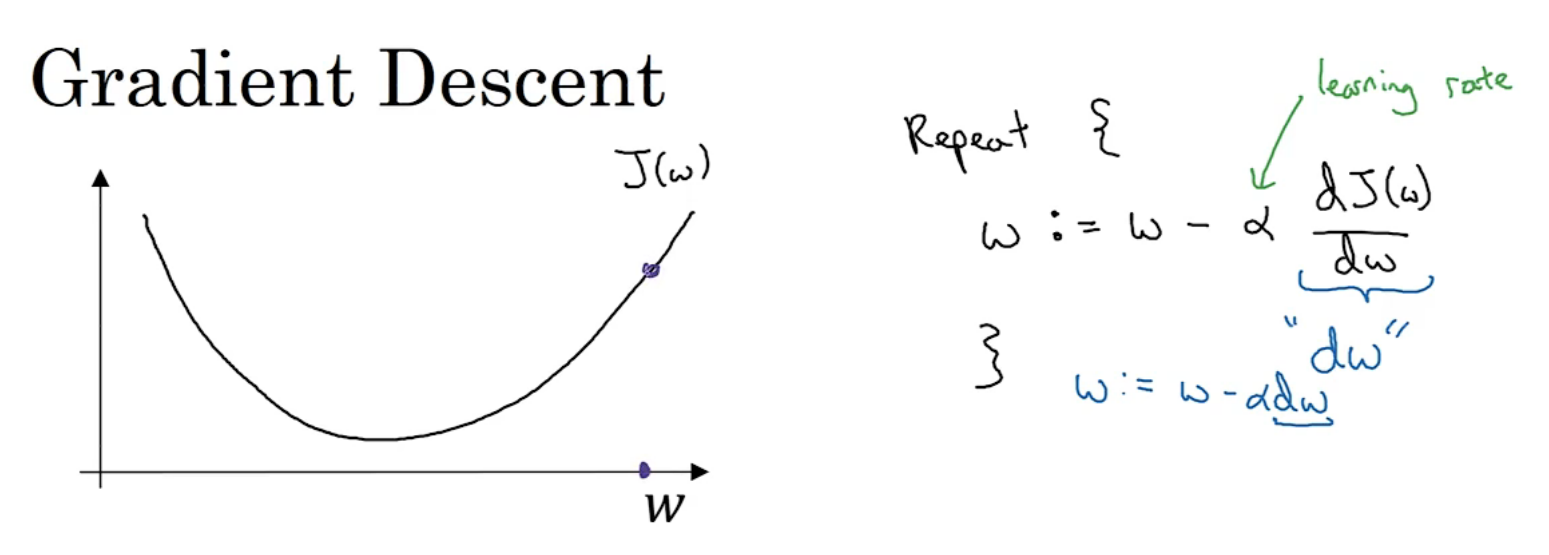
如果考虑到w和b两个参数，就用偏导数，式子大致不变，导数变成对w/b的偏导数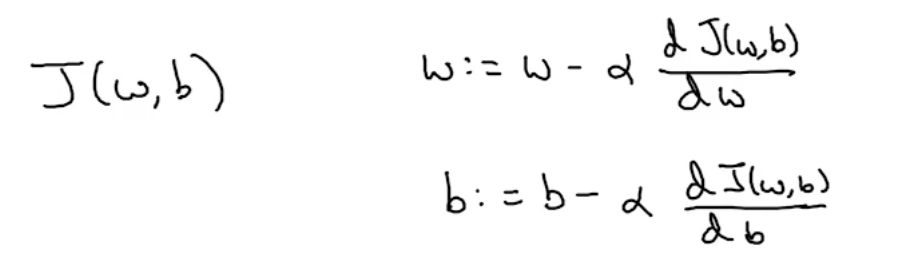

计算图

正向传播 and 反向传播：

首先通过样本正向计算出神经网络的输出，紧接着进行一个反向传输操作，用来计算出对应的梯度，导数

logistic回归中的梯度下降法

eg:只有一个样本的情况

这里感觉有点懵，再解释一下：这里的x1,x2代表一个样本的两个值输入,此处的m就是1，然后初始化w1,w2,b,w也是个矩阵，和x的行数和列数一致，此处是将w置换之后再和x相乘，z应该是一个1 * 1的矩阵，再通过sigmod函数找到y(hat),也是一个1*1的函数，对应该样本的估计y(hat),再通过单个样本的损失函数计算损失

image-20230628223000843

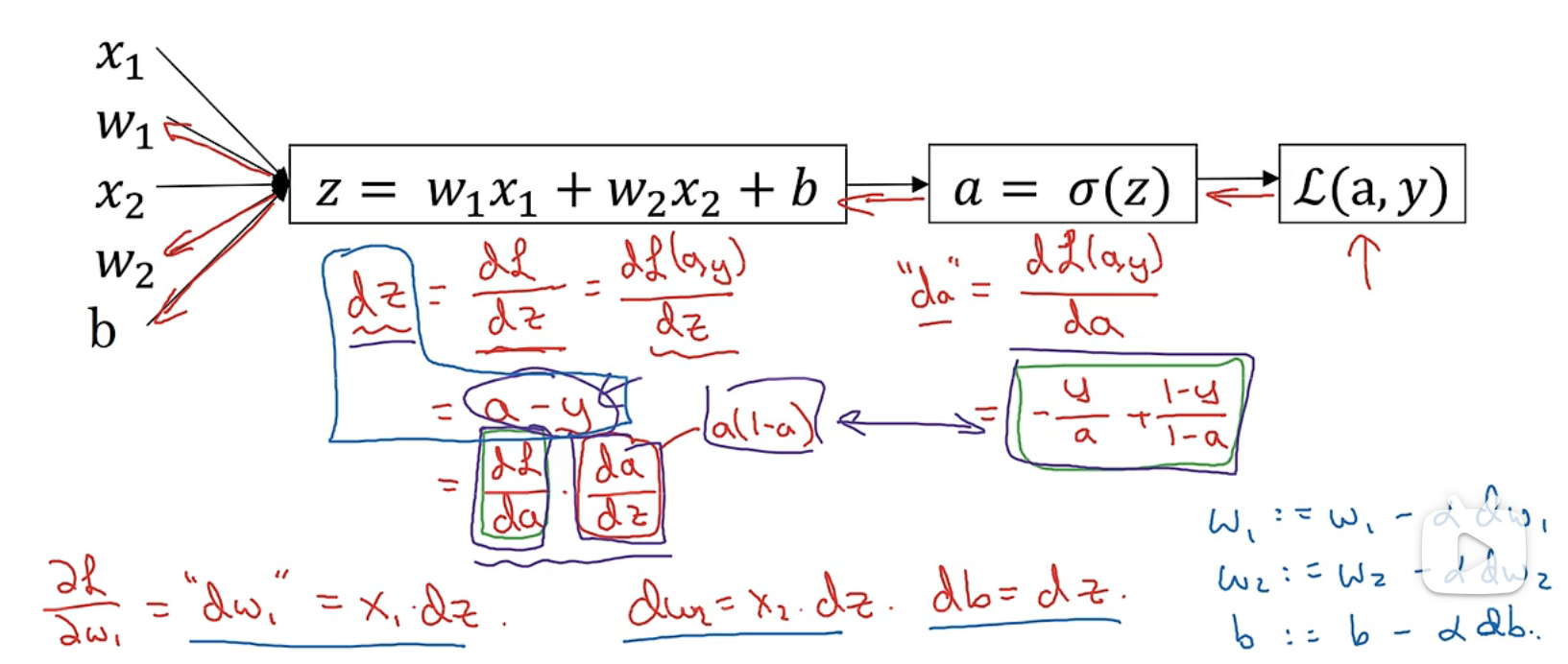
这儿的da/dz不太好理解，列了个式子：

image-20230630162532939

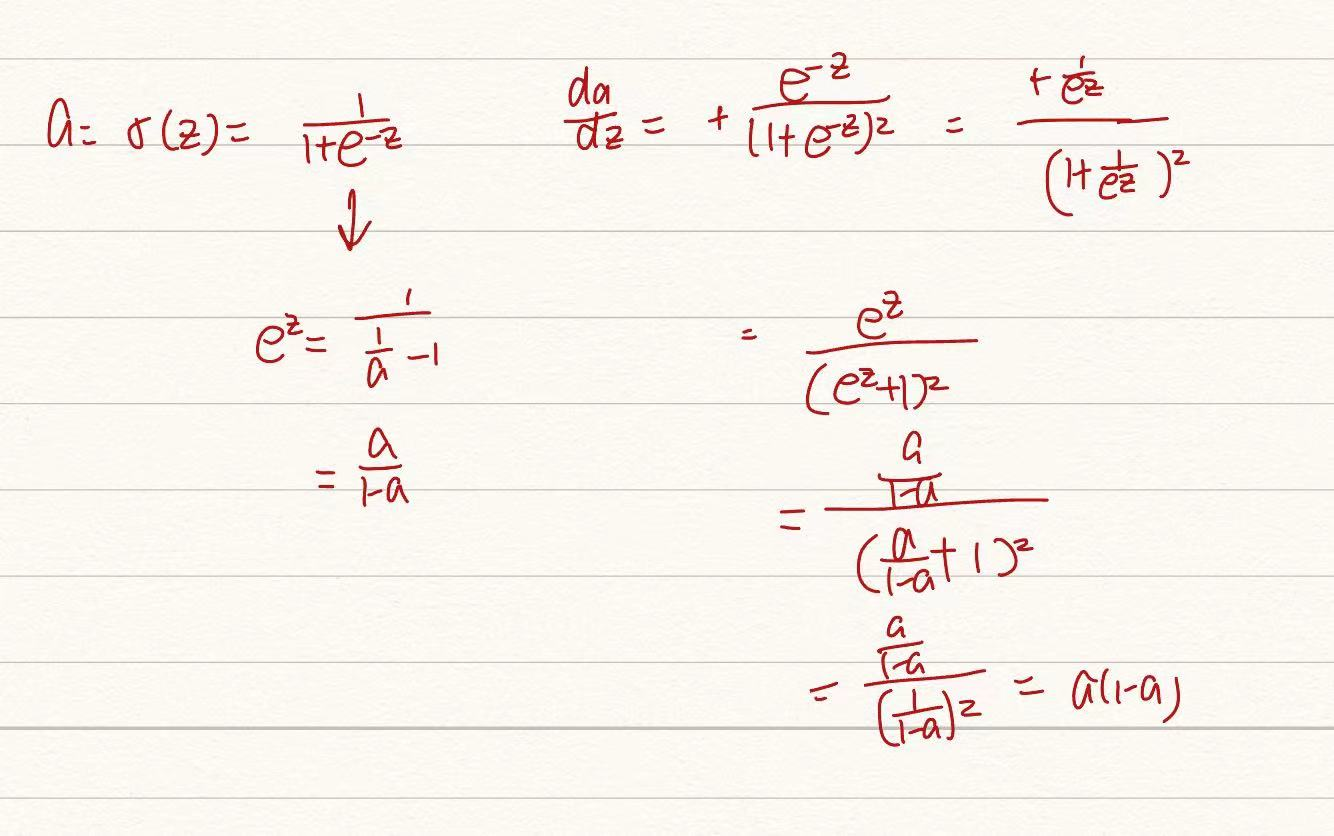
m个样本的梯度下降

正如我们前面所知，成本函数J(w,b)是损失函数平均值，则依然用前面样本的例子J(w,b)对w1求导就是每个样本的损失函数对w1求导的平均值

image-20230628223929648

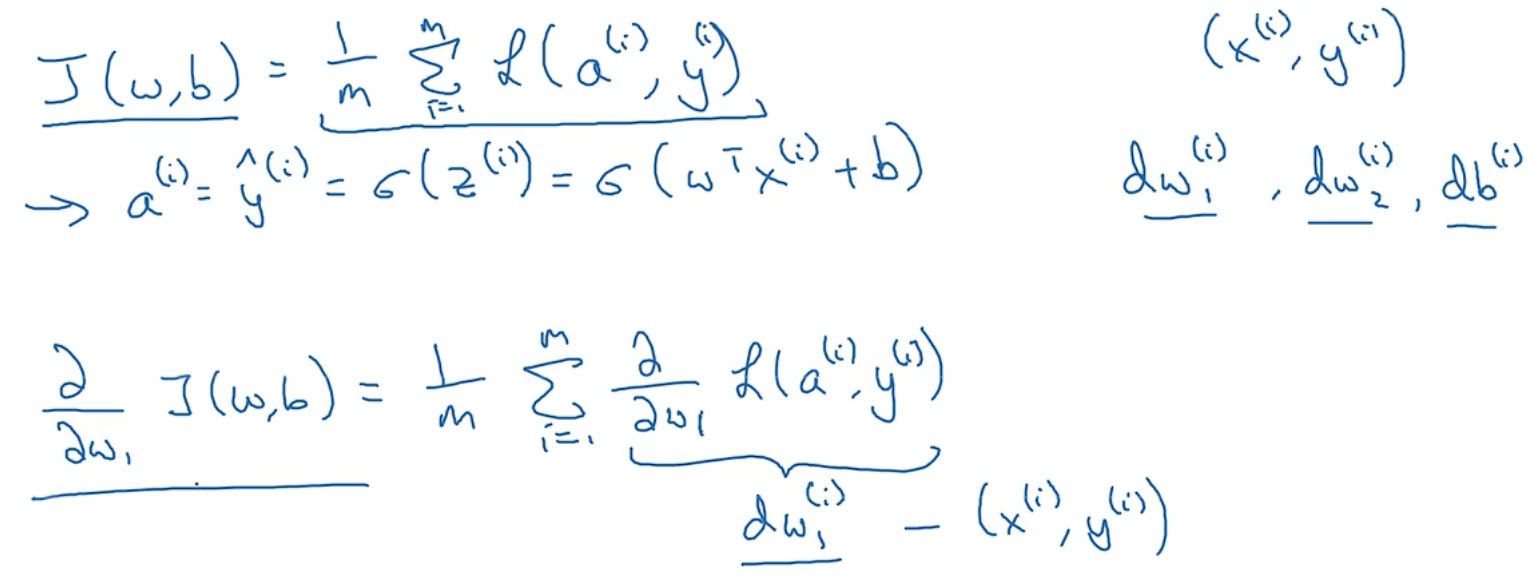
用代码实现：

可以用向量化省去过于冗杂的for循环

伪代码：

J=0
dw=[]
db=0
dz=0
z=[]
a=[]
L=[]
da=[]
dz=[]
for i in range 10000:
    for i in range m:
        z[i]=w(T)*x[i]+b
        a[i]=1/(1+e^(-z[i]))//估计的y值，即y_hat
        L[i]=-(y[i]*log(a[i])+(1-y[i])*log(1-a[i]))//每个样本的损失函数
        da[i]=-(y[i]/a[i]-(1-y[i])/(1-a[i]))//损失函数对a求导
        dz[i]=a[i]-y[i]//损失函数对z求导
        for j in range n:
            dw[j]+=x[i][j]*(a[i]-y[i])
        db+=a[i]-y[i]
        J+=L[i]
    J/=m
    db/=m
    for j in n:
        dw[j]/=m
    for j in n:
        w[j]=w[j]-α*dw[j]
    db=b-α*db

向量化

向量化用于消除for循环，将多组数据放在一个矩阵中共同运算

可扩展深度学习实现可在CPU或者GPU中执行，两者都支持并行（SIMD)

np.dot可快速计算矩阵的乘积，比for快几百倍

向量化的更多例子

等价：

image-20230630170937902

np.exp(v):v矩阵每个元素进行e^运算

np.log(v)

np.abs(v):绝对值

在上面的伪代码中，就可以用向量化代替掉求每个dw[j]的循环

dw不再显示表达，而是用一个矩阵表示:

dw=np.zero((nx,1))
dw+=x[i]*(a[i]-y[i])//这里的x[i]指的是第i个样本的nx*1矩阵

向量化logistic回归

将多个样本用一个矩阵表示

image-20230630173643895

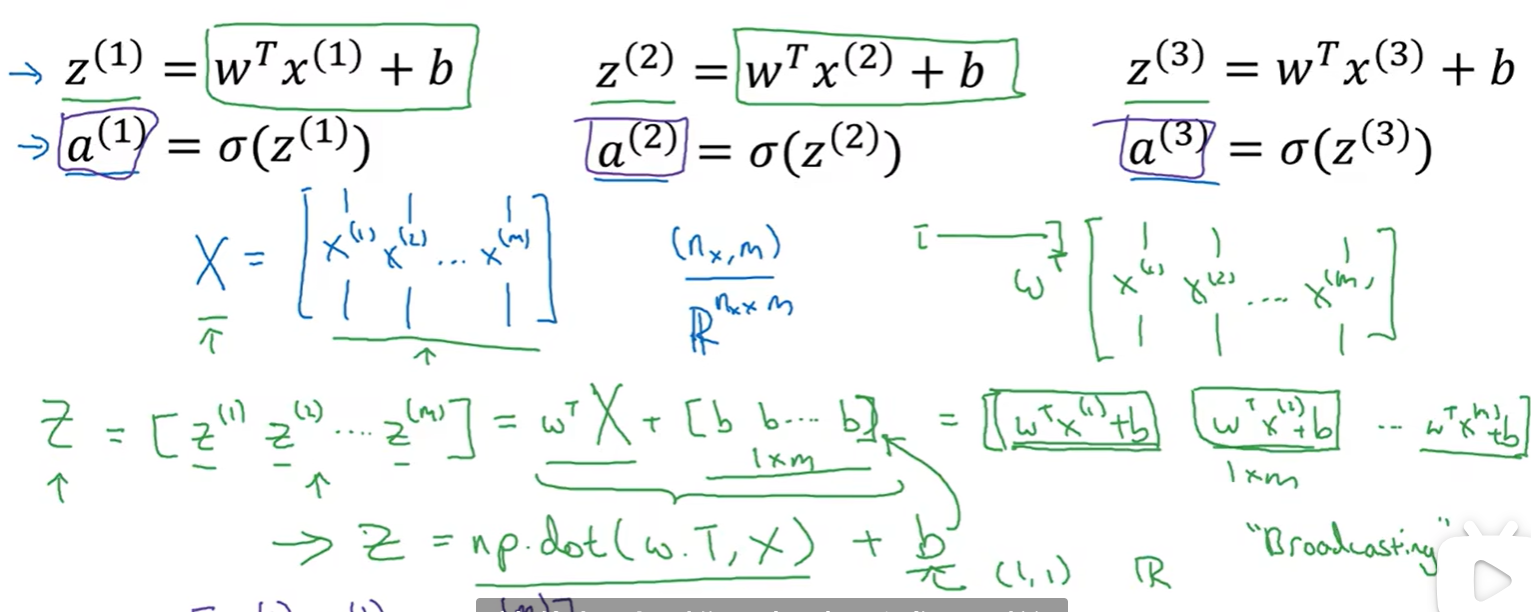
细节解释：这里用了一个矩阵加一个实数，在python中，该实数会根据前面的矩阵扩展成对应形式，即前面的矩阵的每一项都会加上b，然后得到一个新的矩阵

​ 伪代码：

A=np.zero((1,m))//m个样本
W=np.zero((nx,1))//x有n个特征
X=np.zero((nx,m))//nx个特征，m个样本
Y=np.zero((1,m))
dW=np.zero((nx,1))
for i in range 1000
	A=sigmod(W(T)*X+b)
    dZ=A-y
    dW=X*((A-Y)(T))/m
    db=np.sum(A-y)/m
W=W-α*dW
b=b-α*db

Python中的广播

numpy函数:

cal=A.sum(axis=0):表示将A的每一列相加形成新矩阵，如果是水平轴求和axis=1

percentage=100 * A/cal.reshape(1,4):将A的每一列的每一个值除以cal的对应列，这儿的reshape是为了确保cal是一个1*4的矩阵

python中广播常见例子：

image-20230630182902907

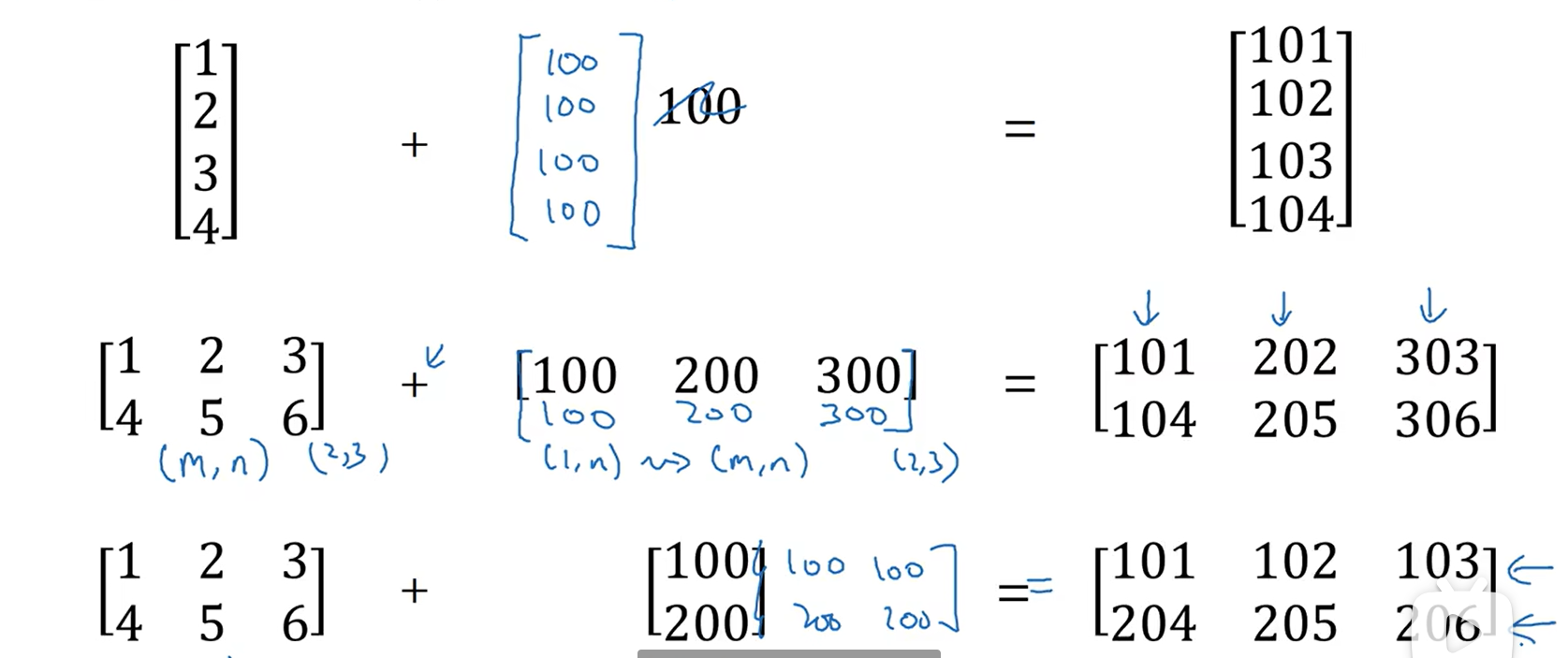
关于python_numpy向量的说明

a=np.random.randn(5)->a.shape=(5,)

a=np.random.rand(5,1)->a.shape=(5,1)

如果定义成了第一种，可以用reshape(5,1)变成(5,1)的

作业

Consider the two following random arrays “a” and “b”:(看一下下面的这两个随机数组“a”和“b”)

a = np.random.randn(4, 3) # a.shape = (4, 3)

b = np.random.randn(3, 2) # b.shape = (3, 2)

c = a * b

What will be the shape of “c”?(请问数组“c”的维度是多少？)

*->对应元素相乘，在该题中，a和b维数不同，不是所有a/b都有对应元素，应该用np.dot

而以下情况会进行广播：

a = np.random.randn(3, 3)

b = np.random.randn(3, 1)

c = a * b->c最后是(3,3)矩阵